4. PRESENTACION Y DISCUSION DE RESULTADOS

4.1. Características de la materia prima

Se caracterizó la pulpa fresca en su contenido de humedad, sólidos solubles (expresado en ºBrix), acidez (expresado mmol NaOH) y pH. Los resultados obtenidos corresponden al promedio de seis repeticiones, las que se muestran en el CUADRO 4.

Humedad. La humedad promedio obtenida en la presente investigación fue de 84,8 ± 0,3 % en pulpa de murta (CUADRO 4).Si se compara con la humedad de la fruta fresca descrita en el CUADRO 1, este valor es superior. Según el modo de preparación de la pulpa, incluyendo además un proceso de escaldado era de esperar que aumente el contenido de humedad. De acuerdo con MUÑOZ (2002) y MERINO (2002) los porcentajes de humedad en pasta de murta son del orden de 82,3 ±1,2 % y 84,1 ± 1,5 %, respectivamente. Por lo tanto, se trabajó con una pulpa de murta similar.

CUADRO 4. Características de la pulpa de murta utilizada para los ensayos.

Sólidos solubles. En relación a los sólidos solubles de la pulpa de murta se obtuvo un valor promedio de 15,2 ± 0,3 ºBrix. Mediciones realizadas por MUÑOZ (2002) en pasta de murta arrojan un valor de sólidos solubles similar (15,2 ± 0,6 ºBrix). TORRES et al.(1999) obtuvieron un valor de sólidos solubles en fruta fresca igual a 19 ºBrix, siendo este valor mayor debido al menor porcentaje de humedad que presenta la murta fresca en relación a la pulpa de murta, aumentando así el contenido de sólidos solubles. La fluctuación del contenido de sólidos solubles en la fruta puede deberse tanto a posibles diferencias de ecotipos de murta, como también al diferente estado de madurez que presente la fruta al momento del ensayo.

Acidez y pH. La acidez obtenida para la pulpa de murta en esta investigación fue de 10,05 mmol NaOH/100 g pulpa de fruta, y encuanto al pH, se obtuvo un valor promedio de 3,73. Valores encontrados en literatura citados por TORRES et al. (1999), hacen referencia a determinaciones realizadas en la fruta fresca, con valores de acidez que fluctúan entre 2,02 a 32,89 meq NaOH en 100 g de fruta fresca por lo que el fruto no presenta una acidez definida.

4.2. Humedad de la pulpa de murta azucarada post secado

El porcentaje de sólidos secos de la mezcla de pulpa de murta y azúcar fue determinado antes del proceso de secado y una vez terminado el proceso. Con el porcentaje de sólidos totales post secado se calculó el contenido de masa seca o de sólido seco que presenta cada uno de los tratamientos, lo que permite la determinación del contenido de humedad de los mismos. Las características de la mezcla azucarada posterior al secado que presenta cada tratamiento corresponden a las características de las láminas de fruta respecto a su contenido de humedad. Los valores obtenidos corresponden al promedio de seis repeticiones, los que se presentan en el CUADRO 5. Se aprecia que los cuatro tratamientos presentan un porcentaje inicial similar de sólidos totales, debido a que los tratamientos presentan la misma composición inicial (85 % de murta y 15 % de azúcar) antes del proceso de secado. Sin embargo, el porcentaje de sólidos totales obtenidos después de la deshidratación presenta una leve variación de los valores promedio, lo que puede deberse a las distintas condiciones de proceso (temperatura, espesor del puré) a que son sometidos los distintos tratamientos durante el secado o debido a una variación natural propia del producto (proceso de difusión al interior del sólido), lo que hace que el proceso de evaporación no sea homogéneo entre tratamientos. Los ensayos fueron realizados en estufa de convección natural hasta un porcentaje de humedad final de un promedio de 15,4 ± 1,1% en las láminas de fruta, aunque el valor de humedad según MERINO (2002) puede alcanzar un porcentaje de 7,1 ± 0,5 % para una misma composición inicial de muestra (85 % de murta y 15 % de azúcar), cuando el secado se lleva a cabo en un secador

CUADRO 5. Características de la mezcla azucarada antes y después del proceso de secado.

de convección forzada con recirculación de aire. Valores de humedad reportados por SAENZ et al. (2003)^Note5. , son del rango de 12 a13 % en láminas deshidratadas. ITDG (2003)^Note6. señala contenidos de humedad hasta un 25 % en láminas de fruta, si éstas se acompañan de un alto contenido de azúcar. Por lo cual, el producto obtenido en este estudio puede ser considerado como una lámina deshidratada, ya que están dentro de un rango de humedad citados en la literatura.

4.3.Determinación experimental de la variación de humedad durante el proceso de secado

El experimento consistió en la determinación de la pérdida de peso de la mezcla durante un lapso de tiempo de alrededor de 50 h hasta alcanzar prácticamente el peso constante. Durante las primeras 30 h se determinó la pérdida de peso a un intervalo de tiempo de 1 hora. A partir de la ecuación 3.1 y considerando los valores de masa seca de cada muestra, se calculó el contenido de humedad promedio de las muestras de fruta con respecto a la masa seca (M_H / M_S) en cada intervalo de tiempo.

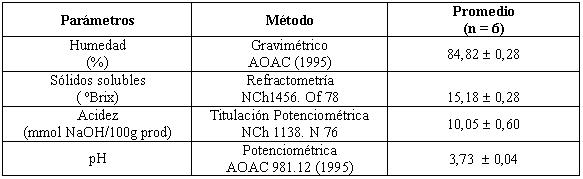
4.3.1. Variación de la humedad en función del tiempo En la FIGURA 3, se muestran las curvas de secado de las láminas de fruta para la humedad promedio (M_H / M_S) en función del tiempo en los diferentes tratamientos (T1, T2, T3, T4). Al observar el comportamiento de secado, las curvas muestran una tendencia de forma polinomial de segundo grado, siendo ésta la que se ajusta con mayor precisión a cada uno de los tratamientos. La humedad varía en función del tiempo desde un valor entre 2,7 y 2,9 kg agua / kg de masa seca hasta un promedio de 0,18 kg agua / kg de masa seca después de las 30 horas de secado. En los tratamientos T1 y T3 con espesor S1 igual a 15 mm, la masa seca varía alrededor de 26 g /100 g de masa húmeda, y en los tratamientos T2 y T4 con un espesor S2 igual a 10 mm la masa seca varía alrededor de lo 18 g / 70 g de masa húmeda.

4.3.2. Comportamiento de secado en los distintos tratamientos. Es posible apreciar una similitud en las curvas correspondiente a cada tratamiento (FIGURA 3), con su coeficiente de correlación cercano a 1. El polinomio correspondiente a cada una de las curvas es válido hasta un tiempo de secado donde la humedad alcanza su valor mínimo, es así como el tratamiento T2 es válido hasta la hora 24de proceso, a partir de este punto la función toma el valor de humedad final. Lo mismo sucede con el tratamiento T4, donde la humedad alcanza su valor casi constante ya en la hora 26, lo que indica que la difusión del agua hacia la superficie del sólido se ve fuertemente reducida a partir de este momento, comenzando las muestras a alcanzar el valor de humedad de equilibrio, así se aprecia en las gráficas correspondientes a los tratamientos señalados.

FIGURA 3. Contenido de humedad en función del tiempo de secado para los cuatro tratamientos.

En el caso del tratamiento T1 y T3 la función toma el valor mínimo después de un tiempo de proceso de alrededor de 36 horas, lo que corresponde al valor de la humedad de equilibrio. Esta diferencia en tiempo de secado entre cada tratamiento tiene relación directa con el espesor de la muestra. Tratamientos T1 y T3 con mayor espesor presentan un tiempo superior de secado para alcanzar el valor de humedad de equilibrio, y a su vez los tratamientos T2 y T4 con menor espesor de muestra requieren de menos tiempo para alcanzar dicha humedad. Al observar la gráfica inferior de la FIGURA 3, se logra apreciar claramente el comportamiento de secado que presentan cada uno de los tratamientos. Tratamientos T2 y T4 con menor espesor presentan un comportamiento similar en sus curvas, que lo diferencia claramente de los tratamientos con mayor espesor. Durante las primeras 10 horas de secado ambos tratamientos presentan una variación de humedad similar en el tiempo, la cual indica que el proceso de secado no depende de las temperaturas de trabajo en este intervalo, luego las curvas comienzan a separase y a medida que transcurre el tiempo empiezan a diferenciarse T2 y T4 y el proceso se ve influenciado por las temperaturas de secado. Respecto a los tratamientos T1 y T3, con mayor espesor de muestra y temperaturas de secado igual a 65 y 55 ºC, se aprecia un comportamiento similar de secado debido al espesor de la muestra. Sin embargo a medida que el tiempo avanza comienzan a diferenciarse ambos tratamientos, siendo la temperatura de secado la que marca tal diferencia. También se observa que la variación de humedad correspondiente a T2 y T4 es más acelerada durante las primeras horas de secado, debido al menor espesor que presenta la muestra, por lo cual el contenido local de humedad presente recorre una menor distancia hacia la superficie de evaporación, si se compara con los tratamientos T1 y T3, con mayor espesor para una misma superficie de secado.

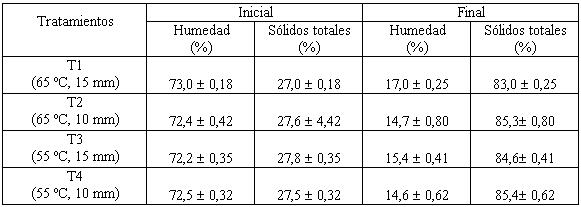
4.3.3. Velocidad de secado en los distintos tratamientos. En la FIGURA 4, se presentan las curvas de velocidad de secado en función de la humedad, donde la ausencia del periodo de velocidad constante se hace evidente al observar las curvas de secado correspondiente a cada uno de los tratamientos, siendo el periodo de velocidad decreciente el que predominó en todo el proceso. La velocidad de secado fue determinada entonces a partir del punto crítico que corresponde a la velocidad máxima de secado, la cual fue calculada según se define en ecuación 3.3. La velocidad de secado aumenta con la temperatura, pero disminuye a medida que el espesor de la muestra aumenta, así se aprecia al observar las curvas correspondiente a los cuatro tratamientos. Por lo cual la velocidad de secado es directamente proporcional a la superficie de secado, e inversamente proporcional al espesor.

FIGURA 4. Curvas de velocidad de secado en función de la humedad promedio para los cuatro tratamientos.

4.4. Determinación de los parámetros de proceso

A partir de las curvas de secado con la humedad promedio en función del tiempo se determinaron los parámetros de proceso, que permiten describir el comportamiento de secado del producto. El tiempo y humedad crítica, la constante de tiempo, humedad de equilibrio y la velocidad máxima de secado correspondiente a cada uno del los tratamientos se presentan en el CUADRO 6.

CUADRO 6. Parámetros de proceso obtenidos a partir de las curvas de secado.

Tratamientos	Punto crítico Constante de tiempo Humedad de equilibrio Velocidad máxima de secado Tiempo crítico Humedad crítica tcr Xcr t* X* (dX/dt)Máx
T1 (65 ºC 15 mm)	1	2,7470	18,8	0,2048	0,1431
T2 (65 ºC 10 mm)	1	2,7799	12,8	0,1747	0,2209
T3 (55 ºC 15 mm)	1	2,6120	20,9	0,1879	0,1217
T4 (55 ºC 10 mm)	1	2,6628	14,1	0,1755	0,1901

Punto crítico. Se observa en el CUADRO 6, un mismo valor de tiempo crítico igual a la primera hora de secado para cada tratamiento, lo que indica que el proceso no consta del primer periodo de secado, o sea, no hay velocidad constante durante el proceso de secado. El tiempo crítico tiene directa relación con la humedad crítica, la cual varía con el espesor del material y con la velocidad de secado (McCABE et al. 1991). Esto muestra diferencias en el punto de inicio del proceso de secado, y como se puede observar en la FIGURA  3 corresponden a 4 diferentes modelos para el proceso de secado. A partir de este momento comienza el periodo de velocidad decreciente.

Constante de tiempo. Se determinó la constante de tiempo según ecuación 3.2, y tal como era de esperarse los tratamientos con mayor espesor presentan una constante de tiempo superior a aquel tratamiento con menor contenido de muestra. También se observa en los valores de la constante de tiempo la influencia de la temperatura sobre cada tratamiento, esto debido a la diferencia de tiempo de proceso que presenta aquellos tratamientos con igual espesor de lámina y distinta temperatura de secado.

Humedad de equilibrio.Con respecto a la humedad de equilibrio esta fue determinada a partir del contenido de sólido seco calculado al final del proceso de secado para cada tratamiento, siendo los tratamientos con mayor espesor los que presentan un mayor contenido de humedad de equilibrio al finalizar el proceso.

Velocidad máxima de secado. Tratamientos con menor espesor de muestra corresponden los valores de mayor velocidad de secado, siendo T2 el que presenta la mayor velocidad de secado con una temperatura de 65 ºC, le sigue el T4 con temperatura de secado de 55 ºC y a continuación tratamientos T1 y T3 con un espesor de muestra mayor y temperaturas de secado de 65 y 55 ºC. Por lo cual la velocidad de secado es directamente proporcional a la superficie de secado, e inversamente proporcional al espesor.

4.5.Simulación del proceso de secado

4.5.1. Determinación del comportamiento del aire de secado. El conocimiento de la condición del aire de secado es de gran importancia en procesos de deshidratación, ya que las propiedades físicas del aire afectan de manera directa sobre la calidad del secado, por lo cual es necesario llevar un control de las variables involucradas, como son: temperatura y humedad relativa del aire de secado. Debido a que fue difícil llevar un control de tales variables se realizó un proceso de simulación para cuantificar el comportamiento del aire durante el tiempo en que duró el experimento. Tal simulación consistió en determinar la variación de la humedad del aire de secado que se produce debido a que el experimento no se realizó con un exceso de aire y además a la abertura de la estufa que se realiza al momento de pesar las muestras.

A continuación en la FIGURA 5, se presenta un diagrama descriptivo del proceso simulado para la determinación del aire de secado.

FIGURA 5. Diagrama descriptivo del proceso simulado.

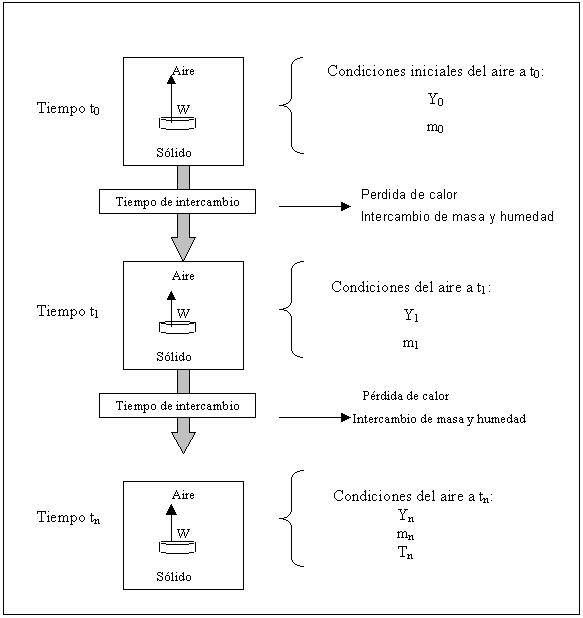
El proceso de simulación involucró las siguientes consideraciones y cálculos:

Consideraciones:

• Condiciones físicas de la estufa de secado: área, volumen
• Condiciones físicas del aire de secado: coeficiente convectivo calor, calor específico, conductividad y difusividad térmica, densidad, y temperatura de bulbo seco
• Condiciones ambientales: temperatura ambiente, humedad relativa

Cálculos:

• Tiempo de intercambio de la masa de aire
• Temperatura del aire de secado al tiempo de intercambio
• Pérdida de calor al tiempo de intercambio
• Pérdida de masa al tiempo de intercambio

Estas permiten la determinación de las masas de aire que salen e ingresan a la estufa en el tiempo de intercambio con sus respectivas humedades, junto con la determinación de la humedad del aire de secado entre cada hora en que se produce la pesada de la muestra, y por tanto la abertura de la puerta. En el ANEXO 1, se presenta una descripción de los pasos a seguir para dichos cálculos. El CUADRO 7, muestra los resultados de la variación que experimenta el aire al tiempo de intercambio, donde se observa que al finalizar la primera hora de secado el aire presenta una humedad relativa de 85 % con una temperatura de secado de 65 ºC, luego al tiempo de intercambio que es igual a 15 s (tiempo de pesada) la temperatura disminuye a 58,7 ºC, debido al intercambio de masa con el medio externo, junto con la pérdida de calor del aire de secado. Ya en la segunda hora la masa y la humedad del aire aumentan, debido al agua evaporada por tiempo de secado y al intercambio de humedad producido durante la pesada, con una humedad relativa de secado de 89 %. Hacia las últimas horas de proceso la humedad relativa del aire disminuye junto con la disminución del agua presente en el sólido, tal como se observa en las curvas de la FIGURA 6.

CUADRO 7. Variación de la humedad del aire al tiempo de intercambio a temperatura de secado de 65 ºC.

Parámetros	Unidades	t0	t1	t2	tn
Temperatura aire de secado	ºC	65	65	65	65
Masa de aire de secado	g	40	45	47	41
Humedad relativa aire de secado	%	80	85	89	15
Tiempo de intercambio	s	15	15	15	15
Pérdida de calor al tiempo de intercambio	J	140,47	140,47	140,47	140,47
Temperatura al tiempo de intercambio	ºC	58,7	58,7	58,7	58,7

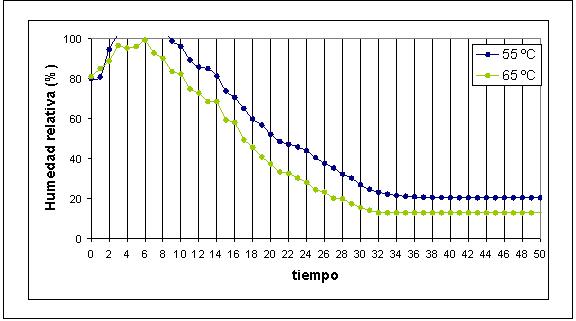
4.5.2. Representación gráfica del comportamiento del aire de secado. La FIGURA 6, representa el comportamiento de la humedad relativa del aire de secado en función del tiempo, donde se aprecia un comportamiento similar para ambas temperaturas de secado durante el transcurso del proceso. Sin embargo, el aire de secado a 55 ºC presenta una humedad de saturación entre la hora 3 y 8 de secado, lo que indica que durante este lapso de tiempo la transferencia de humedad del cuerpo al aire es nula. Luego la humedad relativa del aire comienza a disminuir, junto con la disminución del agua presente en el sólido para ambas condiciones, hasta alcanzar una humedad constante de un 20 % para el secado de 55 ºC y una humedad de 15 % en el secado con aire a 65   ºC. A partir de la hora 31, y hasta el momento en que las muestras son retiradas de la estufa la humedad del aire de secado permanece constante. No hay intercambio de aire debido a que las muestras durante este periodo de tiempo permanecen en las estufas cerradas. La condición del aire se mantiene constante hasta el final del proceso, lo que se puede interpretar también con el término del proceso de secado.

FIGURA 6. Humedad relativa del aire de secado a temperaturas de 55 y 65ºC.

4.6.Parámetros cinéticos adimensionales

El uso de parámetros adimensionales permite relacionar los datos de los diferentes ensayos, reduciendo el número de variables y en consecuencia el número de ensayos necesarios para entender el comportamiento de un proceso. En este trabajo, el cálculo de los parámetros característicosde proceso, tales como punto crítico, constante de tiempo, humedad de equilibrio y velocidad máxima permiten modelar adecuadamente el proceso de secado.

4.6.1. Parámetros adimensionales para humedad y tiempo. Se determinó la humedad (u) y tiempo adimensional () para cada uno de los tratamientos a partir del punto crítico para el periodo de velocidad decreciente. Con las ecuaciones 3.4 que define la humedad adimensional y según ecuación 3.5 correspondiente al tiempo adimensional se obtuvieron los valores adimensionales de los ensayos, los cuales se presentan en la gráfica 1 de la FIGURA 7.

FIGURA 7. Curvas adimensionales de variación de humedad en función del tiempo de secado.

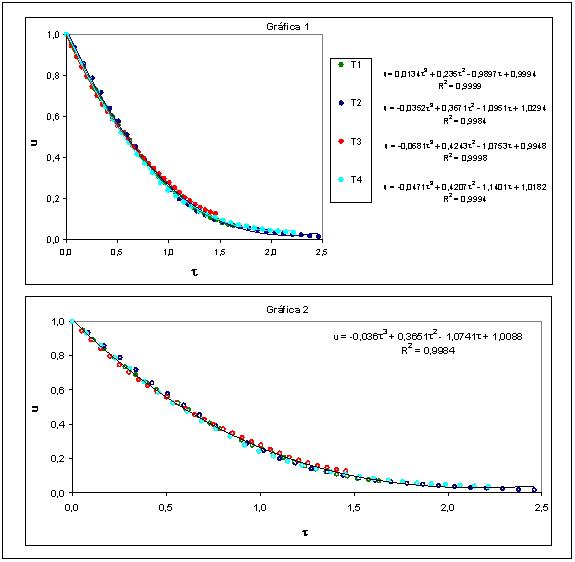
Se ve claramente al observar la gráfica 1, una superposición correspondiente a las curvas de los cuatro tratamientos, por lo cual la variación adimensional de la humedad en función del tiempo no hace diferencia respecto de las condiciones de proceso, ya sea espesor de muestra o temperatura de secado, al contrario de lo que sucede al trabajar con valores de humedad y tiempo absolutos donde existe una clara diferencia entre tratamientos (FIGURA 3). Esta similitud en comportamiento permite relacionar los datos de los distintos tratamientos y obtener una curva común del proceso de secado tal como se presenta en la gráfica 2 de la FIGURA 7. Debido a que se trata de un mismo producto en todos los tratamientos era de esperarse que el comportamiento sea similar bajo cualquier condición de secado. Esto se confirma, ya que los datos obtenidos en los diferentes ensayos se pueden expresar en una curva común (gráfica 2) con un alto coeficiente de correlación muy cercano al valor 1. Se obtiene así una función polinomial, la cual es valida para valores deentre 0 y 2,16. Para un tiempo adimensional mayor, la humedad toma el valor mínimo,. El polinomio obtenido es similar a cada uno de los polinomios de los ensayos por separados (gráfica 1) y corresponde por tanto a un promedio de los resultados de los cuatro experimentos de secado.

4.6.2. Potencial de secado. Considerandoque el experimento cinético clásico se vio afectado por las condiciones exteriores variables es que se introduce un nuevo parámetro adimensional conocido como potencial de secado.

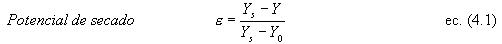
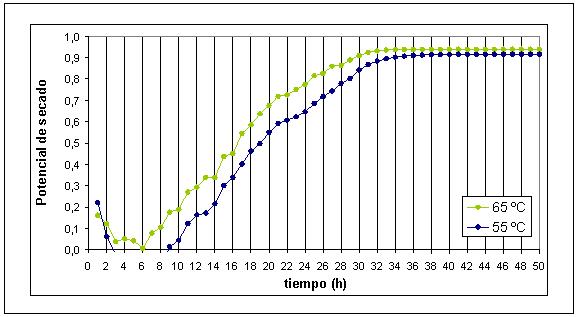
Este parámetro permite conocer el comportamiento de secado que presenta el producto respecto a la humedad del aire de secado. El potencial de secado fue determinado para el transcurso del proceso en ambas estufas, para la condición de secado de 55 y 65 ºC. En la FIGURA 8, se representa el potencial de secado para ambas temperaturas en función del tiempo. Un potencial de secado , significa que el aire de secado tiene una capacidad máxima de secado, mientras el valor de = 0, presenta una mínima. Así se observa en las curvas correspondientes a ambas temperaturas. En el caso de secado con aire a 55 º C entre la hora 3 y 8 de secado el potencial presenta un valor igual a cero, que indica que el secado durante este tiempo es mínimo, debido a que durante estas horas la humedad relativa del aire se encuentra saturada, lo que hace que el proceso de transferencia sea nulo.

FIGURA 8. Potencial de secado en función del tiempo.

Se realizó además una representación del comportamiento que presenta el potencial de secado respecto a la humedad del producto, por lo cual, se obtuvo un perfil del potencial de secado para cada condición de trabajo, la cual se presenta en las curva de la FIGURA 9. Durantes las primeras horas de secado el producto presenta un mayor contenido de humedad, lo que corresponde además a un mayor porcentaje de agua evaporada por hora de secado, presentando el potencial de secado valores menores al inicio del proceso, debido a un alto porcentaje de humedad presente en el aire de secado (FIGURA 6), a medida que la humedad del sólido comienza a disminuir, disminuye la humedad del aire de secado, con lo cual el potencial de secado aumenta. A primera vista se aprecia un comportamiento similar para cada una de las curvas correspondiente a cada tratamiento, pero a la vez la influencia que tiene el espesor de la muestra sobre comportamiento que presenta el potencial de secado se hace presente diferenciando cada una de las curvas. Es así como tratamientos con mayor espesor de lámina, presentan los mayores valores de potencial hacia el final del proceso, si se compara con las curvas de los tratamientos T2 y T4, con menor espesor para una misma humedad del producto, lo que tiene relación con la velocidad de secado que presenta cada uno de los tratamientos, y por tanto al agua evaporada por tiempo de secado.

FIGURA 9. Potencial de secado en función de la humedad adimensional.

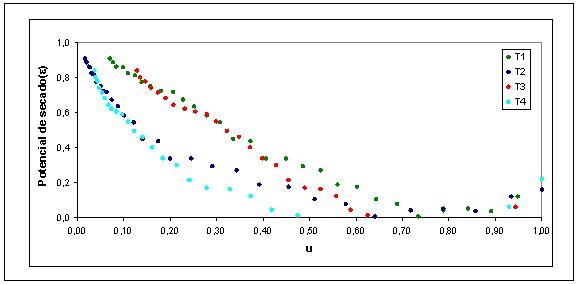
Por lo cual el potencial de secado se relaciona directamente con la humedad del sólido en el momento en que el agua sale de el, y como esta influye en el comportamiento que presenta el aire de secado. Es posible apreciar que tratamientos T3 y T4 a temperatura de secado de 55 ºC, presentan valores de potencial igual a cero, lo que indica una saturación del aire de secado, como se observó en las curvas de la FIGURAS 6 y 8.

4.6.3 Velocidad real de secado y el modelo cinético. A partir del polinomio obtenido en la FIGURA 7, correspondiente a la humedad (u) en función del tiempo (se determinó la velocidad real () para el proceso de secado, la cual se define según ecuación 3.6. La curva correspondiente a la FIGURA 10, representa el comportamiento adimensional de velocidad de secado de la lámina de fruta deshidratada a partir de pulpa de murta azucarada, como una función de la humedad del producto.

FIGURA 10. Velocidad real de secado en función de la humedad adimensional.

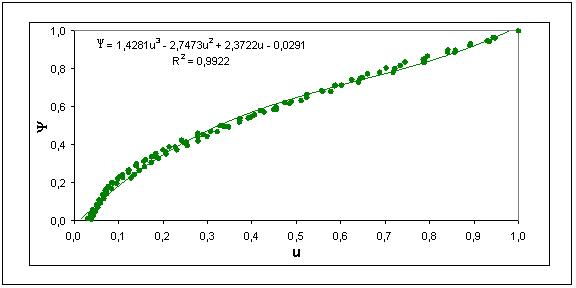
Es así como se obtiene un modelo cinético adimensional (ecuación. 4.2) que representa el comportamiento de secado de un producto, el cual corresponde a una función polinomial de tercer grado, válido para valores de u entre 1 y 0,02 a valores menores de humedad la velocidad alcanza valores negativos, lo que indicaría el efecto higroscópico que presentaría una lámina de fruta hacia las últimas horas de secado. Experimentalmente se ha podido demostrar que al final del proceso de secado, se obtiene un contenido de agua en el producto casi constante lo que corresponde también a una velocidad real de secado igual a cero. Por tanto el modelo tiene su validez sólo hasta la humedad de equilibrio, lo que corresponde en el caso de la lámina de murta a una humedad promedio u igual a 0,02. He aquí la validez de la ecuación 4.2

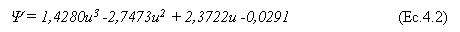
Se tiene entonces un modelo general de secado visualizando como fuerza impulsora la humedad adimensional del aire de secado (ecuación 4.3), la cual se complementa con el potencial de secado

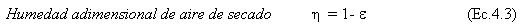
Por tanto la humedad adimensional del aire de secado y a su vez el potencial de secado son función de la humedad adimensional del sólido, tal como se demostró en las curvas de la FIGURA 9. Siendo la velocidad real de secado una función independiente de cualquier condición no constante del proceso, y que sólo depende de la humedad adimensional (u) del producto que se ha secado.

4.7.Determinación del calor específico

El calor específico de una sustancia, es una propiedad termofísica de importancia en procesos térmicos, que en conjunto con la conductividad térmica y la densidad determinan la velocidad de transferencia de calor al interior del producto. Se determinó el calor específico de pulpa de murta azucarada por el método de enfriamiento y por modelos de cálculos existentes en literatura.

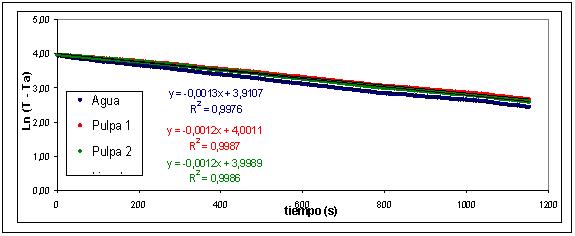
4.7.1. Método de enfriamiento. En la FIGURA 11, se observa una representación gráfica de Ln (T – T_a) en función del tiempo para la pulpa de murta y agua, que se realizó a partir de los datos de enfriamiento obtenidos en la parte experimental. A través de las gráficas se obtuvo el valor de la pendiente (k) correspondiente a cada muestra. Junto con los datos presentados en el CUADRO 8, y según ecuación (3.13) se determinó el calor específico de la pulpa de murta azucarada.

FIGURA 11. Curvas de enfriamiento y valor de la pendiente (k).

CUADRO 8. Datos experimentales obtenidos durante el ensayo para estimación del calor específico.

Mediciones	Unidades	Valores
kagua		0,0013
k1pulpa		0,0012
k2pulpa		0,0012
Masa agua(MH2O)	kg	0,0501816
Masa pulpa1 (Mm)	kg	0,0564163
Masa pulpa2 (Mm)	kg	0,0564074
Masa cilindro de cobre (Mcu)	kg	0,2040607
Calor específico agua (CpH2O)	kJ/kg K	4,1868
Calor específico cobre (Cpcu)	kJ/kg K	0,383

4.7.2. Modelos existentes en literatura

Se estimó el calor específico de la pulpa de murta azucarada mediante relaciones empíricas, modelos basados en la humedad o composición proximal.

A continuación se presenta en el CUADRO 9, lo valores de calor específico obtenidos por los modelos anteriormente mencionados.

CUADRO 9. Calor específico de pulpa de murta azucarada.

Método	calor específico (kJ/ kg K)	Factor
Ley de enfriamiento de NEWTON Muestra 1 Muestra 2	2,32 2,32	1 1
CHOI Y OKOS a 55 ºC a 65 ºC	3,52 3,51	1,5 1,5
DICKERSON	3,49	1,5
SIEBEL	3,26	1,4
CHARM	3,46	1,5

Como es posible apreciar en el cuadro anterior existe una diferencia en el valor del calor específico obtenido experimentalmente, y aquellos obtenidos por modelos existentes en literatura, con un factor de diferencia mayor de 1,5 en caso de CHOI Y OKOS y un factor menor de 1,4 en caso de SIEBEL. Esta diferencia puede estar dada debido a las condiciones experimentales. La incorporación de aire que se produce al momento de mezclar el contenido de azúcar en la pulpa de murta para la obtención de una muestra homogénea, puede haber influido en forma significativa en el volumen de mezcla a utilizar al momento del ensayo, influyendo además en el valor de calor específico obtenido.Respecto a la diferencia de calor específico entre modelos encontrado en literatura, esta se debe a que algunos autores en sus modelos empíricos solo consideran la humedad del producto y otros como CHOI Y OKOS, consideran dentro del modelo la composición proximal para una misma estimación de calor específico. Sin embargo, ambos modelos suministran resultados satisfactorios bajo cierta condición de temperatura y humedad. LAGOS (2002) determinó el calor específico en pasta de murta, mediante el método de las mezclas obteniendo un valor de 3,47 kJ / kg K, y al estimar el calor especifico de la pasta de murta según CHOI Y OKOS, se obtiene un valor de 3,73 kJ / kg K, el cual es mayor que el valor obtenido en pulpa de murta azucarada utilizando igual método de estimación. Este menor valor de calor específico en pulpa de murta tiene relación con el menor contenido de humedad que presenta la pulpa azucarada respecto a la pasta de murta, ya que a medida que el contenido de agua decrece, el calor específico también disminuye. La presencia de aire en la pulpa azucarada, la cual es un material poroso es la causa más probable que el calor específico determinado experimentalmente no coincida con lo valores estimados en literatura, en los cuales no se considera el efecto del contenido del aire en las muestras. En cálculos de consumo energético más detallados se podría considerar el efecto del aire sobre el calor específico de las muestras, pero en cálculos iniciales estimativos para un proyecto de factibilidad económica , es suficiente utilizar modelos de cálculos existentes en literatura . No obstante, el método de enfriamiento de Newton puede entregar valores de calor específicos que se aproximan mejor a la de condiciones reales de procesamiento de un producto como láminas de murta. Será necesario implementar más ensayos para obtener datos válidos estadísticamente.

4.8. Estimación del consumo energético

Para la estimación del consumo energético en la deshidratación de una lámina de fruta, se consideró cada uno de los tratamientos y se evaluó su comportamiento energético bajo distintas condiciones de secado, como la humedad del aire, temperatura de secado y espesor del puré. Se consideraron humedades relativas del aire de secado de 80, 60 y 40% y temperaturas de secado de 65 y 55 ºC (condiciones constantes de proceso). A partir de la ecuación 4.4 que define el coeficiente de vaporización (kg aire/ m²h) y según ecuación 4.5 correspondiente al flujo de calor (kJ / m²h), se estimó el consumo energético en la deshidratación de una lámina de fruta bajo condiciones constantes de proceso (FIGURA 12).

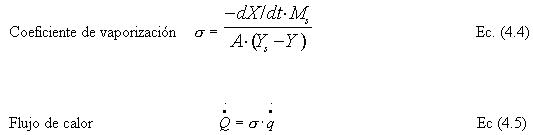
FIGURA 12. Consumo energético de los cuatro tratamientos bajo distintas condiciones del aire de proceso.

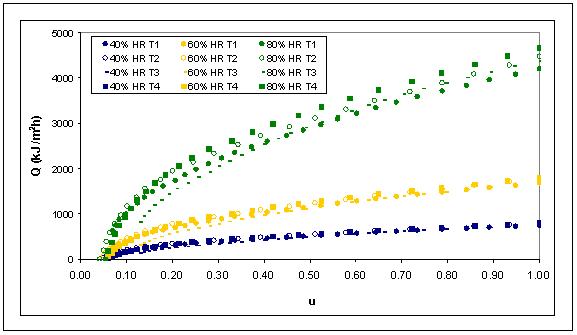
El comportamiento energético estimado se refleja claramente en la curvas de la FIGURA 12, donde se observa que el secado con aire a 80% de humedad relativa, es el que más consume energía, lo cual está dentro de la lógica esperada, debido a que a mayor humedad del aire de secado mayor será el tiempo requerido para la deshidratación de un producto, y por tanto mayor el gasto de energía. Luego con un gasto energético menor se encuentra el secado con aire a 60 y 40 % de humedad relativa. Se observa además en cada una de las curvas que la condición de temperatura y espesor que presentan cada uno de los tratamientos no es significativo en el gasto energético, como si lo es la condición de humedad del aire de secado. Como es de esperarse, a medida que la humedad del producto disminuye el gasto energético también disminuye.

Tiempo de secado: En la determinación del tiempo de secado de la lámina de fruta deshidratada, se utilizó el método de integración gráfica en la que el valor inverso de la velocidad () se representa en función del contenido de humedad (u). (GEANKOPLIS 1986).

FIGURA 13. Representación gráfica del inverso de la velocidad en función de la humedad.

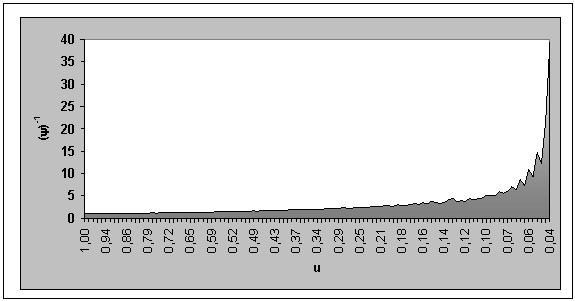
Por lo que el tiempo de secado para cualquier región entre u₁ y u₂ está dado por la ecuación 4.6

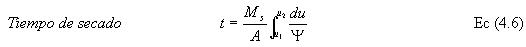
Por tanto, el tiempo promedio estimado para la deshidratación de la pulpa de murta azucarada con una humedad inicial de 73 % y una humedad promedio final en la lámina deshidratada de 15 % es de 11,5 horas de secado bajo condición constante de proceso.

Cálculos energéticos: Con un balance simple de materia y energía y mediante el uso del diagrama de Mollier, se determinó la temperatura de la superficie del producto, la temperatura del aire de calentamiento, y el consumo de vapor para distintas condiciones de proceso.

Condiciones de proceso:

Estado del aire fresco: 20 ºC, 90% HR

Estado del aire a la salida: 40 ºC, 40, 60 y 80% HR

Cantidad de pulpa a secar: 1000 kg / h

Humedad inicial de la pulpa de fruta: 73%

Humedad final de la lámina de fruta deshidratada: 15%

Balance de materia: Se determinó la cantidad de agua evaporada por hora de secado, donde W = 682 kg agua evaporada/h y por tanto la cantidad de producto deshidratado es igual a 318 kg de láminas por hora de secado.

CUADRO 10. Valores energéticos obtenidos a través del diagrama de Mollier.

PARAMETROS	UNIDADES	Humedad relativa del aire de secado 40 % 60 % 80 %
Entalpía	KJ/ kg aire seco	87	113	138
Temperatura superficie	º C	28	32	37
Temperatura aire calentamiento	º C	53	76	102
Consumo de vapor	KJ / h	59334	77066	94116

Los valores energéticos estimados indican que la condición del aire de secado es uno de los parámetros fundamentales a considerar al momento de deshidratar un producto, tal como se aprecia en el CUADRO 10, valores de entalpía estimados señala un gasto mayor en kJ por kg de aire seco para la condición de humedad relativa 80 % y a la vez un mayor consumo de vapor por hora de secado, junto con un aumento de la temperatura de calentamiento. A medida que la humedad del aire disminuye, la entalpía, la temperatura de calentamiento y consumo de vapor requerido para el proceso de secado se ve fuertemente reducido.