Profesores Informantes
Sr. Erwin Carrasco Ruiz – Ingeniero Civil Químico – Instituto de Ciencia y Tecnología de los Alimentos.
Sr. Fernando Figuerola R. – Ingeniero Agrónomo, M. S. Food Science – Instituto de Ciencia y Tecnología de los Alimentos.
Reseña
Cuando trabajáis sois como una flauta a
Través de cuyo corazón el murmullo de las
Horas se convierten en música
K. Gibran
RESUMEN
El objetivo de esta investigación fue obtener un modelo para la cinética del proceso de secado en la elaboración de una lámina de fruta (“fruit leathers”) a partir de la murta (Ugni molinae Turcz) por el método cinético experimental y realizar cálculos del consumo energético en la deshidratación. Se trabajó con pulpa de murta mezclada con azúcar en una relación de 85 % murta y 15 % azúcar. Se implementaron mediciones de humedad en ensayos de secado a dos distintas temperaturas con dos distintos espesores de producto. El procedimiento de elaboración consistió en la selección, el lavado, el escaldado y el despulpado de la fruta, la mezcla de los ingredientes y la deshidratación. Las láminas se deshidrataron hasta alcanzar una humedad final de aproximadamente 15 %. Se calcularon los parámetros de proceso como punto crítico, humedad de equilibrio, constante de tiempo y velocidad máxima de secado, los que permiten la determinación de los parámetros adimensionales del proceso (humedad y tiempo), junto con la obtención del modelo cinético. Se realizó un proceso de simulación para conocer el comportamiento del aire de secado debido a la condición no constante del proceso. Se determinó el calor específico de pulpa de murta azucarada por el método de enfriamiento de Newton y por modelos matemáticos existentes en literatura, además de realizar cálculos del consumo energético en la deshidratación.
SUMMARY
The objective of this tesis was to obtain a matematical model for the kinetics of the drying process in the elaboration of a fruit láminas (fruit leathers") from murta (Ugni molinae Turcz) though an experimental kinetic method. Futhermore calculations of the energy consumption during the dehydration process were carried out. Pulp of murta was blended with sugar in a relation of 85% murta to 15% sugar. Experimental measurements were conducted at two temperatures for two different thickness. The elaboration procedure consisted on the selecting, washing, blanching and pulping of the fruit, thereafter mixing the ingredients before starting the dehydration process. The laminas were dehydrated until an aproximate humidity of 15% in the final product was achieved. Process parameters calculated were critical point, balance humidity, time constant and maximum drying rate, whereupon adimensionals process parameters (humidity and time), necessary for establishing the kinetic model, were derived. A simulation process was also carried out in order to estimate the behaviur of the drying air due to the non constant process condition. The specific heat of sweetened murta pulp was determined according to Newton’ s law of cooling and the results were compared to specific heat values calculated from exiting models in literature. Thereupon, calculations of the energy consumption during the dehydration process carried out.
NOMENCLATURA
| Símbolo | Unidades | |
A |
área | m2 |
| Cpa | calor específico aire | J /kg K |
| Cpag | calor específico agua | J /kg K |
| Cpcu | calor específico cobre | J /kg K |
| Cpm | calor específico de la pulpa de murta azucarada | J /kg K |
| dX/dt | velocidad de secado | kg / kgh |
| (dX/dt)max | velocidad de secado máxima | kg / kgh |
| Fo | número de Fourier | _ |
| HR | humedad relativa el aire | % |
| h | coeficiente convectivo de calor | W /m2 K |
| k | conductividad térmica | W /m K |
| (k) | pendiente | _ |
| MH | masa húmeda del sólido | kg |
| MS | masa seca del sólido | kg |
| m | masa de aire | kg |
| Q | flujo de calor | W |
| q | flujo específico de calor | J |
| S | espesor | mm |
| T | temperatura en el instante t | ºC |
| Ta | temperatura ambiente | ºC |
| T0 | temperatura inicial | ºC |
| t | tiempo en el instante t | h |
| t0 | tiempo inicial | h |
| tcr | tiempo crítico | h |
| t* | constate de tiempo | _ |
| u | humedad adimensional | _ |
| V | volumen | m3 |
| w | masa de agua | kg / kg |
| X | contenido de humedad promedio | kg / kg |
| X0 | contenido de humedad inicial | kg / kg |
| Xcr | contenido de humedad crítica | kg / kg |
| X* | contenido de humedad de equilibrio | kg / kg |
| Y | humedad del aire en el instante t | kg / kg |
| Y0 | humedad inicial del aire | kg / kg |
| Ys | humedad de saturación del aire | kg / kg |
| Y | fracción másica | kg / kg |
| α | difusividad térmica | m2/ s |
| ρ | densidad | kg / m3 |
| ε | potencial de secado | _ |
| τ | tiempo adimensional | _ |
| ψ | velocidad real de secado | _ |
| σ | coeficiente de vaporización | kg / m2h |
| η | humedad adimensional del aire de secado | _ |
| subíndice | ||
| w | agua | |
| c | carbohidratos | |
| m | cenizas | |
| f | fibra | |
| L | lípidos | |
| P | proteínas | |
| s | sólido | |
1. INTRODUCCION
Son ampliamente conocidas las ventajas de los productos vegetales deshidratados ya que al reducir el contenido de humedad de ellos disminuye notablemente la actividad microbiológica y aumenta la vida útil del producto, además de disminuir los costes de almacenamiento y transporte.
Las láminas deshidratadas aparecen como un atractivo método alternativo para extender la vida útil de frutas procesadas. Estas son elaboradas a partir de la deshidratación de purés de fruta mezclados generalmente con azúcar.
El estudio de cinética de secado es esencial para diseñar un correcto proceso de secado lo que permite obtener un producto de calidad. Además, puede considerarse como una herramienta muy eficiente para evitar daños al producto, consumo excesivo de energía, desgaste del equipo o la disminución del rendimiento.
Como hipótesis en este trabajo se postuló que:
A través de la determinación de la cinética de secado por el método cinético experimental, será posible obtener informaciones útiles para optimizar el consumo de energía en la elaboración de una lámina de fruta a partir de la murta.
Objetivo general:
- Obtener un modelo para la cinética del proceso de secado en la elaboración de una lámina de fruta (“fruit leathers”) a partir de la murta (Ugni molinae Turcz) por el método cinético experimental y realizar cálculos del consumo energético en la deshidratación.
Objetivos específicos:
- Determinar la cinética del proceso de secado en muestras de murta a diferentes temperaturas y espesor del puré
- Determinar el calor específico del puré de murta por el método de enfriamiento y por modelos de cálculo existentes en la literatura
- Estimar el consumo energético en el proceso de deshidratación durante la elaboración de una lámina de fruta a partir de la murta
2. REVISION BIBLIOGRAFICA
2.1. Características generales de la murta
La murta o murtilla es una planta endémica que crece en forma silvestre en el centro y sur de Chile, pertenece a la familia de las Myrtaceae, género Ugni, siendo la de mayor importancia Ugni molinae Turcz o murta roja (TORRES et al., 1999). La especie crece en forma espontánea, de preferencia en lugares asoleados y secos, aún cuando también se le encuentra a orillas de cursos de agua (LAVIN y MUÑOZ, 1988). Se distribuye desde Talca, VII Región hasta el río Palena, XII Región (RODRIGUEZ, 1986), presentando un vigoroso crecimiento y abundante fructificación, lo que está demostrando su adaptabilidad a un clima de tipo templado lluvioso con una marcada influencia marítima (Montaldo, citado por SEPULVEDA, 1994). De acuerdo con LAVIN y MUÑOZ (1988) el periodo de cosecha de la murtilla se extendería normalmente desde fines de marzo a mayo y debe realizarse cuando los frutos presentan un color rojo uniforme y aroma fragante.
La murtilla presenta buenas características para ser industrializada, debido a la peculiaridad del sabor y aroma de su fruta. La principal forma de comercialización de este fruto es en fresco, no obstante sus características hacen de el una buena alternativa para la elaboración de productos procesados comestibles.
La murta es un fruto pequeño y liviano, de epicarpio color rojo y pulpa blanco. Entre las características físico químicas mencionadas por TORRES et al. (1999), el fruto presenta un contenido de sólidos solubles de 19 %, un pH de 4,29 y una acidez titulable de 8,2 meq NaOH en 100 gramos de producto. Según MERINO (2002) el contenido de sólidos solubles presenta una variación respecto a lo mencionado por TORRES et al (1999) el cual es de 13,5 %, el pH posee un valor de 3,35 y la humedad del puré de fruta alcanza un valor de 84 %.
La composición química de la murta se observa en el CUADRO 1.
CUADRO 1. Composición química de la murtilla.
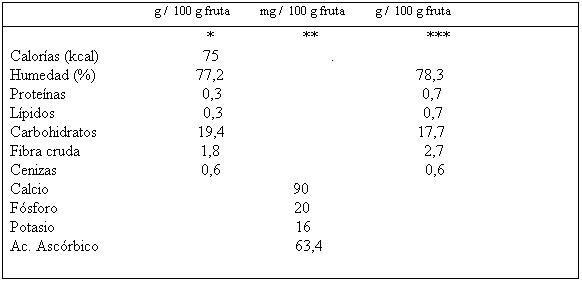
FUENTE:
* SCHMIDT – HEBBEL y PENNACCHIOTTI, (1979)
** TORRES et al., (1999)
*** Comunicación interna del ICYTAL, año 2002
2.2. Deshidratación de vegetales
La deshidratación es el proceso mediante el cual se extrae el agua que posee un producto, bajo condiciones controladas de temperatura y humedad de secado. El propósito fundamental de la deshidratación como medio de conservación de los alimentos es la reducción de la actividad de agua en el alimento, mediante la disminución del contenido hídrico, a niveles inferiores a aquellos que permite el desarrollo de los microorganismos (VAN ARSDEL et al., 1973). La eliminación del agua de frutas y vegetales por deshidratación constituye un método muy indicado para inhibir el crecimiento de microorganismo y, al mismo tiempo, inactivar las enzimas si se acompaña de pretratamientos complementarios (BELITZ y GROSCH, 1997).
El sistema más ampliamente utilizado para lograr la deshidratación de frutas y verduras es a través de calefacción y evaporación del agua por una corriente de aire caliente sobre el cuerpo o la masa. Los productos deshidratados ofrecen variadas ventajas sobre los productos frescos, por ejemplo la reducción de la masa y del volumen, como también el aumento de la vida útil.
El secado de vegetales con altas temperaturas provoca reacciones de degradación principalmente afectando las propiedades organolépticas del producto y su valor nutricional por lo que la temperatura de secado es una variable a tener en cuenta en los estudios cinéticos, pues aunque temperaturas elevadas pudieran acelerar el proceso, la pérdida de calidad del producto no compensaría la reducción del tiempo de proceso (VEGA et al., 2002a)Note1. . Desde este punto de vista es muy importante la temperatura y el tiempo de proceso. Con el objeto de preservar el color del producto deshidratado, la temperatura no debe sobrepasar los 75 ºC.
El pardeamiento no enzimático y la pérdida de pigmentos antociánicos que ocurre durante el secado son la mayor causa de degradación de color en productos vegetales. Con tiempos de secado prolongados se obtienen productos de baja calidad debido a la caramelización de azúcares, la reacción de Maillard, las reacciones enzimáticas, la degradación de pigmentos y la oxidación del ácido ascórbico. Para reducir al mínimo las alteraciones de color, aroma y sabor, originadas por las reacciones de oxidación y otros cambios de carácter químico, es preciso deshidratar el producto hasta un contenido de agua residual muy bajo, por lo general inferior al 5% (GAHONA, 2002)Note2. .
La selección de las condiciones de secado apropiadas son necesarias para minimizar el efecto de alta temperatura, eliminar el resecado y mantener los componentes que determinan la calidad del producto (carotenoides, vitamina C, tocoferoles y otros). En este contexto, interesa estudiar las características del fenómeno a fin de determinar las condiciones precisas para llevar a cabo la deshidratación industrial en el tiempo mínimo, con el mejor resultado y mayor economía posibles, aprovechando al máximo el calor, sea en la fase de transmisión al aire de secado, o bien en aquella durante la cual el aire lo suministra al vegetal en el secador.
2.3. Láminas de frutas
La deshidratación comercial de frutas ha tenido un importante incremento en los últimos años, y una de sus aplicaciones son las láminas de frutas, las que se obtienen mediante remoción de agua de una extensa capa de fruta hasta obtener la estructura de una lámina, tal como lo hizo MOYLS (1981) con puré de manzana. Las láminas son elaboradas por la deshidratación de purés de frutas. Estas pueden ser preparadas de muchos frutos, y una serie de combinaciones de ellos. También pueden ser endulzadas, por la adición de azúcar o saborizadas con la adición de especias (ITDG, 2003)Note3. . La preservación de láminas de fruta depende del bajo contenido de humedad, típicamente 15 a 25 %, la acidez natural de la fruta y el alto contenido de azúcar. El producto tiene una vida útil superior a 9 meses si las condiciones de secado han sido las correctas y el envasado el adecuado. Cuando la lámina de fruta no es correctamente empacada, pierde color y sabor gradualmente y los estándares de calidad son difíciles de mantener (Woodroof citado por MERINO, 2002).
El tiempo de secado varía según el tipo de deshidratación con que se lleve a cabo el proceso, de 6 a 8 horas en un deshidratador, sobre 18 horas en un horno de secado, y de 1 a 2 días bajo secado solar (ITDG, 2003)5, por lo general se utiliza el aire caliente como medio secador, debido a su abundancia, conveniencia y a que puede ser controlado fácilmente mediante equipos adecuados (Torres citado por MERINO, 2002).
La temperatura de secado es un factor a considerar, la cual varía entre 45 y 121 ºC. Sin embargo, altas temperaturas provocan problemas de caramelización por lo que no son aconsejables a pesar de reducir considerablemente el tiempo de proceso.
2.4. Proceso de secado
Se entiende por secado el procedimiento adoptado para eliminar el agua de un producto, térmicamente por evaporación a través del mecanismo de conducción o convección de calor, este procedimiento involucra un cambio de fase de liquido a vapor. (KNEULE, 1966).
2.4.1. Características del material por secar. Para la elección de un método de secado es preciso tener en cuenta la naturaleza de la sustancia y su estado: sólido, pastoso o líquido. En el caso de sustancias sólidas existen tres tipos de sólidos: a) porosos, los que contienen liquido principalmente en el interior de los poros; b) sólidos no porosos, comprenden geles coloidales, donde la humedad es generalmente parte integral del cuerpo sólido, y distribuida en éste homogénea o heterogéneamente y c) sólidos cristalinos, tal como los cristales de sacarosa después de la centrifugación, los cuales no contienen liquido en el interior y el secado tiene lugar solamente en la superficie del sólido (McCABE, et al., 1991).
La disponibilidad de agua en una sustancia varía de un producto a otro según su composición.Bajo este contexto se define:
Agua libre: corresponde a la diferencia entre el contenido de agua del sólido y el contenido de agua de equilibrio. Se comporta como agua pura, encontrándose en estado líquido, la cual es retenida en la superficie del sustrato seco en los poros sólo por fuerzas de capilaridad.
Agua ligada: es el líquido retenido por un sólido que ejerce una presión de vapor menor que la del líquido puro a la misma temperatura, encontrándose el agua en estado rígido (PERRY, 1958).
Entre varias materias se distinguen las que son higroscópicas a cualquier grado de humedad y las que sólo lo son después de haber alcanzado un determinado grado de humedad. Entendiéndose por material higroscópico el que puede contener humedad ligada y por material no higroscópico el que no puede contener nada de humedad ligada.
2.4.2. Estado del aire utilizado en secadores convectivos. En cualquier proceso de secado cabe considerar el efecto de las variables externas sobre las características de proceso. La cantidad de aire utilizado debe ser de importancia suficiente con respecto a la del producto para que el estado del aire no se vea en la práctica influenciado por el calor cedido al producto y a la humedad que ha absorbido. Bajo este supuesto cabe considerar:
Presión parcial de vapor de agua: corresponde en el estado de equilibrio a la presión del vapor de agua en una mezcla vapor aire (KNEULE, 1966). Para estimar la presión parcial de vapor en el aire se utiliza la ley de Dalton, según la cual la presión parcial de un componente es directamente proporcional a la fracción molar del componente en el aire:
pi = yip
Siendo :
pi: presión parcial del componente i
yi: fracción molar del componente i
p: presión total del sistema
Humedad relativa: todo cuerpo en contacto con un ambiente absorbe o pierde humedad si no hay una igualdad entre las presiones parciales de vapor de aire circundante y del cuerpo húmedo. La importancia o magnitud de esta diferencia depende esencialmente de la humedad relativa del aire, la que indica cuánto se aparta el estado del aire húmedo del estado de saturaciónNote4. .
Temperatura: es una medida de la cantidad de energía del aire, el cual provee el calor que posibilita la evaporación del agua presente en el alimento. Cuanto mayor sea la diferencia de temperatura entre el aire y el producto, mayor será la cantidad de calor transferido.
Bulbo húmedo y seco: una forma simple de determinar la humedad relativa del aire utilizado para secar un producto en un secador de convección es la determinación de las temperaturas del bulbo húmedo y seco. La diferencia de temperatura entre el bulbo seco y el bulbo húmedo del aire indica el grado de saturación del aire. Si esta diferencia es cero el aire se encuentra saturado y no existe mayor capacidad de retención de vapor de agua por parte del aire y el secado no se produce (VAN ARSDEL, 1973). Para el caso de que es válida la consideración de un enfriamiento adiabático donde la entalpía del aire y temperatura de bulbo seco es igual a la entalpía y temperatura de bulbo húmedo, se puede afirmar en forma práctica que el calor que traspasa el aire al sólido es utilizado para convertir el agua en vapor, y luego el calor latente de vaporización es traspasado nuevamente al aire manteniendo así la entalpía del aire constante.
2.5. Estática de secado
La estática evalúa el proceso de secado a través de balances de masa y de energía en determinados instantes sin considerar la velocidad del proceso. Permite reconocer entre otros si hay pérdidas excesivas en el sistema y estimarlas, y tomar en consecuencia las medidas apropiadas para optimizar el proceso. En el siguiente esquema se presenta un balance de masa y energía que describe el proceso de secado adiabático en estado estacionario.
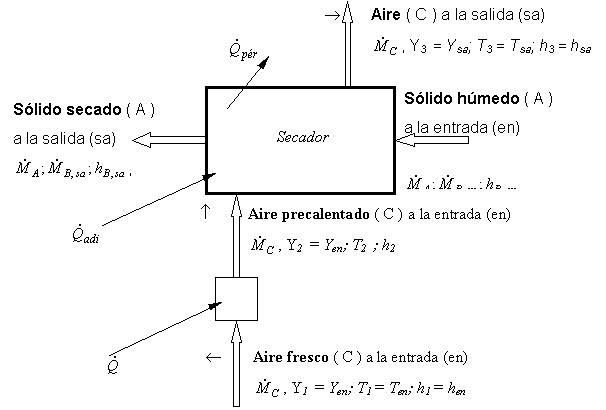
siendo: A sólido, B agua, C aire ,Y humedad del aire, h entalpía
en estado estacionario se tiene:
Balance de masa:
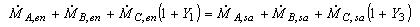
Balance de entalpía:
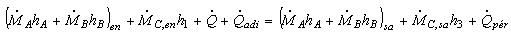
suponiendo un flujo de masa constante para el sólido (A) y el aire (C)
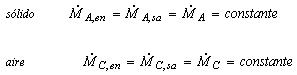
2.6. Cinética de secado
La cinética de secado es de gran utilidad, ya que permite el estudio del proceso de secado bajo condiciones controladas. Además es esencial para un correcto diseño del proceso de secado, lo que permite obtener un producto de calidad. La descripción de la cinética de secado contempla:
Movimiento de la humedad: la transferencia de masa, es decir del agua, ocurre durante el secado como líquido, vapor o ambos dentro del sólido y vapor desde las superficies húmedas. La resistencia a la transferencia de materia, y no a la transmisión de calor, puede controlar la velocidad de secado (McCABE,et al.,1991).Al igual que en otros procesos de transferencia, como transferencia de masa, el proceso de secado de materiales debe considerarse desde el punto de vista de las relaciones de equilibrio (aire-vapor de agua y el material sólido) y además, de las relaciones de velocidad (GEANKOPLIS, 1986).
Difusión dentro del sólido: dependiendo de la naturaleza del sólido el secado puede basarse tanto en el mecanismo interno de la circulación del líquido como en el efecto de las condiciones externas. En el caso de sólidos no porosos este periodo puede ser descrito por un modelo de difusión y para sólidos porosos por un modelo de flujo capilar.
Modelo de difusión: es característico de los materiales que se secan lentamente. La resistencia a la transferencia de vapor de agua desde la superficie del sólido hasta el aire es generalmente despreciable y la difusión dentro del sólido controla la velocidad global de secado. Por tanto, el contenido de humedad en la superficie es muy próximo a la humedad de equilibrio. La velocidad del aire tiene poco o ningún efecto, mientras que su humedad influye sobre el proceso al determinar la humedad de equilibrio (McCABE,et al., 1991). En el modelo de difusión es aplicable la segunda ley de Fick que describe el comportamiento de humedad en un sólido no poroso.
Modelo de flujo capilar: se puede suponer que un lecho empacado de esferas no porosas contiene espacios vacíos entre dichas esferas que se llaman poros. A medida que se evapora el agua, las fuerzas capilares se ponen en acción debido a la tensión interfacial entre el agua y el sólido. Estas fuerzas proporcionan la fuerza impulsora para el movimiento del agua a través de los poros hacia la superficie de secado, el agua puede fluir desde regiones de concentración elevadas hasta las de bajas concentraciones como resultado de una acción capilar en lugar de difusión, por lo cual es aplicable la primera ley de Fick en lugar de la segunda
2.6.1. Periodo de secado de velocidad constante.El secado de un producto húmedo comienza muy a menudo por un periodo de velocidad de secado constante. Este fenómeno se refiere a una humectación más o menos completa de la superficie del producto en el que el proceso de secado viene determinado por la transferencia de materia sobre esta superficie (KNEULE, 1966). Durante este periodo, el flujo de calor intercambiado entre el aire y el producto se utiliza enteramente para la evaporación del agua. Este periodo continúa mientras que la superficie del producto esté alimentada por agua libre líquida desde el interior. En la mayoría de los casos esta etapa de velocidad de secado constante finalizará cuando el contenido de humedad del producto alcance el valor de la humedad crítica (CASP y ABRIL, 1999).
2.6.2. Punto de inflexión o punto crítico.A medida que disminuye el contenido de humedad, termina el periodo de secado a velocidad constante, y la velocidad de secado disminuye. El comienzo de este decrecimiento se caracteriza, en general, por una inflexión más o menos acentuada de la curva de secado denominado punto crítico. Este punto marca el instante en el que el agua liquida sobre la superficie es insuficiente para mantener una película continua que recubra todo el área de secado. El contenido de humedad en el sólido corresponde entonces a la humedad crítica, la cual no es una propiedad característica del material, sino depende del tamaño de la muestra y de las condiciones del aire de secado (McCABE, et al., 1991).
2.6.3. Periodo de secado de velocidad decreciente.En este segundo periodo de secado el flujo másico se reduce más rápidamente que en el periodo anterior. La resistencia a la transferencia de materia entre la superficie y el aire que la rodea es ahora despreciable con respecto a la resistencia interior, que hace más difícil el transporte de la humedad al interior del sólido (KNEULE, 1966). Las fuerzas impulsoras de este transporte son las fuerzas capilares y las fuerzas de difusión. En el modelo de flujo capilar se utiliza el número de Biot para cuantificar este efecto y se incluye también un factor de resistencia que relaciona el coeficiente de vapor del agua a una temperatura y presión constante en una capa de aire con el de una capa porosa del sólido, ambas capas siendo de igual dimensiones. Las propiedades de la materia que debe secarse son las que deciden el predominio de una u otras. Esta fase finaliza cuando el producto alcanza su humedad de equilibrio,la cual corresponde a la porción de agua del sólido húmedo que no puede ser separada por el aire, que depende, como es lógico, de las condiciones de secado (CASP y ABRIL, 1999).
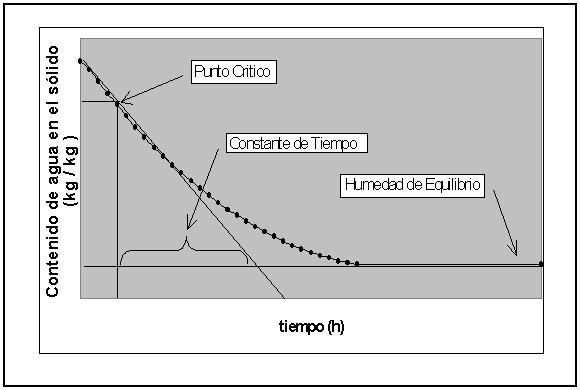
2.6.4. Representación gráfica de los periodos de secado.El estudio de los fenómenos de secado bajo condiciones constantes, se consigue sin hacer variar la temperatura, la humedad y la velocidad del aire que se desplaza sobre la muestra estudiada. Cuando el producto que debe secarse se pesa a intervalos determinados, se obtienen curvas como la de la FIGURA 1 (KNEULE, 1966). La grafica (a), muestra el contenido de humedad del producto en función del tiempo, en la grafica (b) se muestra la variación de la humedad del producto.
FIGURA 1. Curvas del curso del secado en condiciones de secado constante.
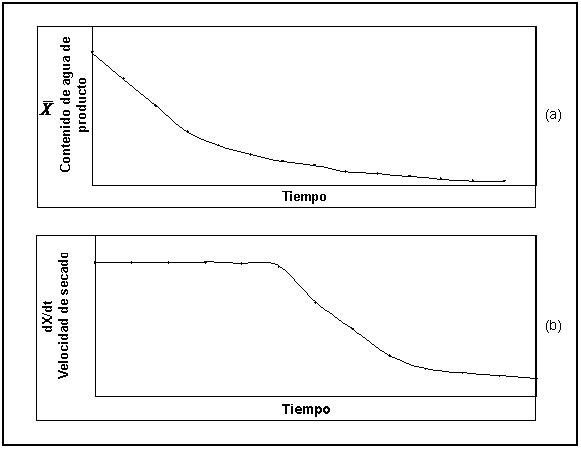
en función del tiempo. Esta variación referida a la superficie se llama velocidad de secado (KNEULE, 1966). La gráfica (b) muestra claramente que el fenómeno el secado se divide en dos periodos, uno a velocidad de secado constante o casi constante y el otro en que esta velocidad presenta una disminución.
2.7. Experimento cinético clásico
Una alternativa existente en la evaluación de procesos de secado es el método cinético clásico experimental, en el cual el exceso de aire es la característica primordial durante el proceso de secado, y, que permite mantener el secado bajo condiciones constantes de proceso como son temperatura y humedad del aire de secado. En la evaluación del experimento cinético clásico, se usan parámetros adimensionales para describir el comportamiento de secado del producto. La determinación de las variables adimensionales como humedad, tiempo y velocidad de secado, pueden ser utilizados en modelos generales de proceso, y sirven de fundamento para el diseño de equipos como también para la simulación de condiciones variables de trabajo. Se puede implementar un experimento cinético clásico en estufas de secado si se asegura que la humedad absorbida por el aire no causa cambios relevantes en la humedad del aire.
2.8.Calor específico
Se define el calor específico como la cantidad de energía requerida para aumentar en un grado la temperatura de una unidad de masa. En el sistema internacional de unidades, SI, el calor específico tiene la unidad J/kg K. Cuanta más capacidad calorífica tenga un cuerpo menor incremento de temperatura requerirá para un mismo aporte de calor. De forma general el calor específico varía en función de la temperatura, como también en función de los componentes de la sustancia. Por tanto, en la literatura especializada existen varios modelos para el cálculo del calor específico. A continuación se describe algunos de los modelos más utilizados. El CUADRO 2 presenta un resumen de algunos modelos.
La mayoría de los modelos contempla el calor específico con función del contenido de humedad, lo que se justifica por la presencia de agua en los productos alimenticios. Debido a que el calor específico del agua demuestra una variación con la temperatura (LIDE, 1999; PERRY et al., 1999), se espera también una variación del calor específico de los productos alimenticios con la temperatura, aunque muy moderadamente.
Un método experimental básico para determinar el calor específico es el método de la mezcla, que consiste en el intercambio de calor entre un cuerpo caliente y otro frío hasta el equilibrio térmico. Este método es muy conocido en la literatura y ha sido utilizado por varios autores para la determinación del calor específico de muchos productos alimenticios (HWANG y HAYAKAWA, 1979, MOHSENIN,1980).
CUADRO 2. Modelos matemáticos para la estimación del calor específico de productos alimenticios.
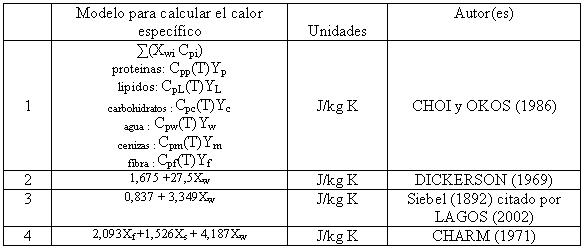
También aparece como método alternativo para la determinación del calor específico de una sustancia, los métodos basados en la ley de enfriamiento de Newton, el cual consiste en comparar la velocidad de enfriamiento de una sustancia con la del agua cuyo calor específico es conocido, la ley establece que la rapidez de variación de temperatura es proporcional a la diferencia de temperatura del cuerpo menos la del medio ambiente.
Otro método, más sofisticados que los anteriores, es la determinación del calor específico por el calorímetro diferencial – Differential Scanning Calorimeter, técnica en la cual la diferencia de energía aplicada a los materiales de muestra y referencia se mide como una función de temperatura, mientras la sustancia y el material de referencia están sujetos a un programa controlado de temperatura (Mc NAUGHTON y MORTIMER, 1975). Este método está basado en la medición de efectos térmicos muy pequeños, producidos durante el proceso térmico.
3. MATERIAL Y METODO
La parte experimental del estudio se llevó acabo en los laboratorios del Instituto de Ciencia y Tecnología de Alimentos (ICYTAL), de la Facultad de Ciencias Agrarias, Universidad Austral de Chile, Valdivia.
3.1. Material
3.1.1. Materia prima. La materia prima utilizada es murta (Ugni molinae Turcz), proveniente de la zona de Punucapa, Valdivia. De la murta fresca se elaboró una pulpa, la cual se mantuvo congelada. El azúcar blanco (sacarosa) se adquirió en un supermercado de la cuidad.
3.1.2. Equipos. Para los ensayos se utilizaron los siguientes equipos:
- Medidor y Registrador de temperaturas, COLE-PALMER, Digi-Sense® de 12 canales
- Computador, EPSON, modelo Q 201ª utilizado como monitor
- Termocuplas, COLE-PALMER, Kapton ® tipo T, rango -250 a 404 ºC
- Termómetros de mercurio, BRANNAN, de -20 a 110 ªC, ± 1 ºC
- Estufa de secado, HORO 035
- Horno de aire caliente, GELLENKAMP, cat 04010
- Despulpadora, STERLING ELECTRIC, NC # AA1H2D
- Potenciómetro, RADIOMETER COPENHAGEN
- Refractómetro, BELLIGHAN AND STANLEY, modelo RF330.
- Balanza electrónica FY3000, Precisión 0,1g
- Balanza analítica, CHYO JK200, Precisión 0,0001g
- otros utensilios de laboratorio, tales como: desecador, pinzas, cápsulas de aluminio, reactivos (hidroxido de sodio), arena tratada, pie de metro etc.
3.2. Metodología
3.2.1. Diseño experimental. Se aplicó un diseño experimentalde dos factores. El primer factor fue la temperatura, la cual se encuentra a dos niveles (55, 65 ºC) y un segundo factor el espesor, el que también se encuentra a dos niveles (S1 y S2 mm), es decir 4 tratamientos con tres repeticiones cada uno, en total 12 ensayos. A continuación se muestra en el CUADRO 3 el diseño experimental.
CUADRO 3. Diseño experimental.

3.2.2. Tratamientos preliminares a la deshidratación. Son varias las operaciones preliminares a que se debe someter la fruta antes del secado:
- Selección y lavado de la murta: se seleccionó la fruta según el color, el estado físico (entero, firme y sin daños físicos visibles). Se descartó también los restos de hoja, palos y cualquier fruta en mal estado o cualquier resto eventual de insectos que aún pudieran estar presentes, y se realizó un enjuague con agua potable para eliminar suciedad superficial.
- Precalentamiento: se realizó a baño maría hasta que la temperatura de la fruta alcance los 50 ºC
- Despulpado: el despulpado de la murta se realizó en una despulpadora semi industrial con un tamiz de 0,5 mm
- Congelado y almacenamiento: se procedió a congelar la murta ya despulpada y envasada en bolsas de polietileno en cámara congeladora a ‑30 ºC
- Descongelado: la pulpa de murta fue descongelada, con un tiempo previo de 15 horas antes de su utilización en la preparación de las láminas
- Mezclado: en esta etapa se adicionó el azúcar a la pulpa de murta en una relación de 15% azúcar y 85% murta. Se aseguró una buena mezcla repetible en todas las muestras preparadas a través de un control del tiempo de mezcla bajo condiciones similares
- Moldeado: se incorporó la pulpa ya mezclada en los respectivos moldes para su posterior secado. Se controló el peso de las muestras, lo que determina también el espesor de las láminas.
3.2.3. Deshidratación. Se llevó acabo en una estufa deshidratadora. Se realizó un experimentoclásico de cinética de secado, bajo condiciones constante, como son humedad y temperatura del aire de secado. Se trabajó a dos temperaturas de secado 55 y 65 ºC, y a dos diferentes espesores de lámina S1 y S2. Se procedió a colocar una cantidad determinada de muestra en moldes, quedando sólo expuesta a la corriente de secado la superficie de dicha lámina. La pérdida en peso corresponde a la pérdida de humedad durante el secado, la cual se determinó a diferentes intervalos de tiempo.
3.2.4 Determinaciones analíticas. Se realizaron determinaciones analíticas para caracterizar la materia prima a utilizar. Estas determinaciones fueron:
- Sólidos solubles: mediante un refractómetro Bellighan and Stanley RF330 (NCh 1456.Of 78)
- Acidez: se determinó por titulación potenciométrica utilizando NaOH 0,1N (NCh 1138.N76)
- pH: se cuantificó mediante un potenciómetro Radiometer Copenhagen (AOAC 981.12.1995)
- Humedad: se determinó mediante el método gravimétrico (AOAC, 1995)
3.3. Definición de los parámetros del proceso
Para evaluar cualquier proceso es un requisito básico definir los parámetros de proceso. En el presente trabajo se definió parámetros, tales como la humedad promedio, el punto crítico, humedad de equilibrio, la constante de tiempo y la velocidad máxima de secado y también otros parámetros adimensionales.
3.3.1. Humedad promedio. Con los datos obtenidos en el proceso de deshidratación correspondiente a la pérdida de peso, se puede calcular la humedad promedio, X, como la masa de agua en kg por unidad de masa del sólido seco en kg en función del tiempo de secado, y según ecuación 3.1.
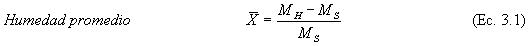
3.3.2. Punto crítico. A partir del gráfico de humedad del sólido con respecto al sólido seco se puede obtener el punto crítico (tcr,Xcr), si corresponde al caso. Este punto delimita las dos zonas del proceso de secado, el periodo de velocidad constante y el periodo de velocidad decreciente. Para la determinación del punto crítico se utilizó un método gráfico numérico, tomando los primeros valores de la curva de secado y aplicando el método de regresión lineal. Los valores de la curva que se ajustan a la recta con valor del coeficiente de correlación igual a uno corresponden al período de velocidad constante de secado. El punto crítico es el punto donde termina la recta del periodo de velocidad constante y se inicia el segundo período de secado a velocidad decreciente.
3.3.3. Humedad de equilibrio. La curva de secado sigue generalmente un curso asintótico hacia el final del proceso, lo que permite determinar la humedad de equilibrio (X*). Es la humedad final del producto en equilibrio con la humedad del aire. En este punto se termina el proceso de secado convectivo. La humedad que se logra eliminar por el aire es reabsorbida por el producto.
3.3.4. Constante del tiempo. Se puede definir además un parámetro del tiempo, conocido como la constante del tiempo, t *, la cual corresponde a la razón entre la capacidad máxima de secado y la velocidad máxima de proceso. Este parámetro es también un tiempo ficticio utilizado para caracterizar el proceso de secado de un producto. Es el tiempo que demoraría el proceso de secado desde el inicio del ensayo en condición estacionario hasta alcanzar la humedad de equilibrio, si la velocidad de secado fuese constante en todo el proceso. En la FIGURA 2 se puede apreciar la recta de extrapolación para obtener la constante del tiempo, t*, y también el punto de bifurcación correspondiente al punto crítico del experimento. Se debe tener en cuenta que el estado estacionario del experimento se logra recién cuando el sólido haya alcanzado la misma temperatura del aire de secado.
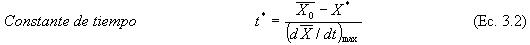
3.3.5. Velocidad máxima de secado. La velocidad máxima de secado corresponde a la máxima cantidad de agua evaporada respecto a su cantidad de masa seca por tiempo de secado, es decir la capacidad máxima de proceso por tiempo de secado.
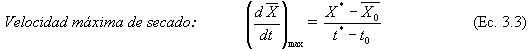
FIGURA 2. Representación gráfica de un proceso de secado ilustrando los parámetros de proceso.
3.4. Definición de parámetros adimensionales
La evaluación de proceso involucra generalmente ensayos con múltiples variables, por lo que conviene reducir el número de variables para disminuir en consecuencia los números de ensayos experimentales. La determinación del punto crítico, la constante del tiempo, y humedad de equilibrio, permiten la definición de variables adimensionales para el proceso de secado, los cuales pueden ser utilizados en modelos generales del proceso.
3.4.1. Humedad adimensional. Este parámetro considera la variación de humedad con respecto a la variación máxima de la humedad en el ensayo. En el periodo de velocidad decreciente la humedad puede variar desde la humedad en el punto crítico hasta la humedad de equilibrio. La diferencia entre la humedad en el punto crítico y la humedad de equilibrio corresponde a la cantidad máxima de humedad que puede ser eliminada en el proceso. Es un valor constante característico del producto, lo cual se utiliza como valor de referencia, y que permite evaluar el comportamiento de diversos productos con humedades iniciales diferentes. Se define según expresa la ecuación 3.4.
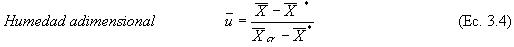
3.4.2. Tiempo adimensional. En el segundo período de secado con velocidad decreciente, el tiempo necesario para una reducción constante en la humedad de producto varía durante el proceso. A menor velocidad de secado, mayor será el tiempo de secado para la eliminación de una misma cantidad de humedad. Por tanto, en la modelación del proceso de secado es conveniente relacionar el tiempo absoluto de secado con la constante de tiempo, el cual depende de la velocidad máxima de secado. Se obtiene así un parámetro de tiempo, en el cual se relativiza el tiempo en función de la misma velocidad de secado. El tiempo adimensional para el proceso de secado en el periodo de velocidad decreciente se define en la ecuación 3.5.
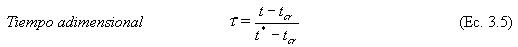
3.4.3. Velocidad real de secado.Es un concepto utilizado en la modelación del proceso de secado. En la representación adimensional tiene el significado de un factor empírico para corregir la velocidad de secado en el segundo periodo. La velocidad real de secado es una función de la humedad.
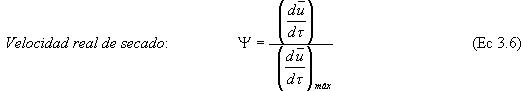
3.5. Determinación del calor específico
El calor específico del puré de murta fue determinado empleando la ley de enfriamiento de Newton, el cual consiste en comparar la velocidad de enfriamiento del puré de murta con la del agua, cuyo calor específico es conocido. Cuando la el calor transferido en la unidad de tiempo hacia el cuerpo por conducción, convección y radiación es aproximadamente proporcional a la diferencia de temperatura entre el cuerpo y el medio externo.

siendo :
α : coeficiente de intercambio de calor
A : área de cuerpo
T : temperatura en el instante t
Ta : temperatura ambiente
Si la temperatura T del cuerpo es mayor que la temperatura del medio ambiente Ta, el cuerpo pierde una cantidad de calor dQ en el intervalo de tiempo comprendido entre t y t + dt, disminuyendo su temperatura T en dT.

siendo :
m: masa del cuerpo
Cp: calor especifico
La ecuación que describe la variación de la temperatura T del cuerpo en función del tiempo es
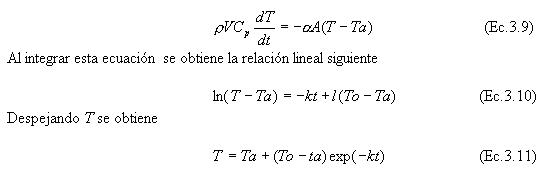
Si se mide la temperatura del cuerpo durante su enfriamiento a intervalos de tiempo, y se realiza una representación gráfica de ln (T- Ta) en función de t, los puntos se ajustaran a una linea recta, de pendiente -k
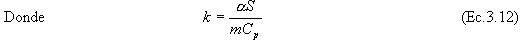
A partir de los datos obtenido en la parte experimental, se realizó una representación gráfica de ln (T - Ta) en función del tiempo para el caso de la pulpa de murta y el agua, a partir de la cual se obtuvieron los valores del las pendientes (k) para ambos casos y según la ecuación 3.13, se determinó el calor especifico de la pulpa de murta azucarada
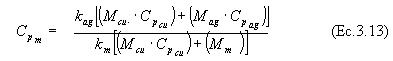

3.6. Cálculo del consumo energético
Con los datos adquiridos sobre el proceso de secado, se realizaron cálculos de consumo de energía bajo varias condiciones de operación y se determinó los parámetros más apropiados para el proceso de secado, tales como la humedad del aire de secado, la temperatura de secado y/o el espesor del producto.
4. PRESENTACION Y DISCUSION DE RESULTADOS
La elaboración de láminas de frutas consiste principalmente en un proceso de deshidratación de la pulpa de fruta mezclada con azúcar. La calidad del producto final depende mucho de la elaboración de la misma mezcla como también del proceso de deshidratación. En este trabajo fueron diseñados experimentos para modelar el comportamiento de secado de una mezcla típica de pulpa de murta azucarada sin semilla para la preparación de láminas de fruta. Se determinó la cinética de secado, y considerando las condiciones variables de un proceso de secado técnico se elaboró el modelo cinético. Los ensayos se realizaron con un producto específico diseñado para obtener una lámina de fruta a partir de la murta. Consiste en una receta de 85 % de murta y 15 % de azúcar, lo que según MERINO (2002) se obtiene un producto con alta aceptabilidad y estabilidad microbiológica en el tiempo.
4.1. Características de la materia prima
Se caracterizó la pulpa fresca en su contenido de humedad, sólidos solubles (expresado en ºBrix), acidez (expresado mmol NaOH) y pH. Los resultados obtenidos corresponden al promedio de seis repeticiones, las que se muestran en el CUADRO 4.
Humedad. La humedad promedio obtenida en la presente investigación fue de 84,8 ± 0,3 % en pulpa de murta (CUADRO 4).Si se compara con la humedad de la fruta fresca descrita en el CUADRO 1, este valor es superior. Según el modo de preparación de la pulpa, incluyendo además un proceso de escaldado era de esperar que aumente el contenido de humedad. De acuerdo con MUÑOZ (2002) y MERINO (2002) los porcentajes de humedad en pasta de murta son del orden de 82,3 ±1,2 % y 84,1 ± 1,5 %, respectivamente. Por lo tanto, se trabajó con una pulpa de murta similar.
CUADRO 4. Características de la pulpa de murta utilizada para los ensayos.
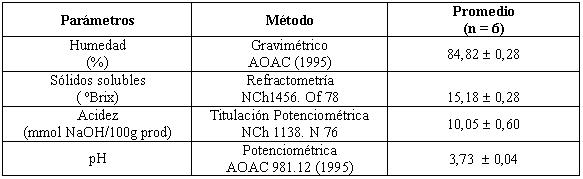
Sólidos solubles. En relación a los sólidos solubles de la pulpa de murta se obtuvo un valor promedio de 15,2 ± 0,3 ºBrix. Mediciones realizadas por MUÑOZ (2002) en pasta de murta arrojan un valor de sólidos solubles similar (15,2 ± 0,6 ºBrix). TORRES et al.(1999) obtuvieron un valor de sólidos solubles en fruta fresca igual a 19 ºBrix, siendo este valor mayor debido al menor porcentaje de humedad que presenta la murta fresca en relación a la pulpa de murta, aumentando así el contenido de sólidos solubles. La fluctuación del contenido de sólidos solubles en la fruta puede deberse tanto a posibles diferencias de ecotipos de murta, como también al diferente estado de madurez que presente la fruta al momento del ensayo.
Acidez y pH. La acidez obtenida para la pulpa de murta en esta investigación fue de 10,05 mmol NaOH/100 g pulpa de fruta, y encuanto al pH, se obtuvo un valor promedio de 3,73. Valores encontrados en literatura citados por TORRES et al. (1999), hacen referencia a determinaciones realizadas en la fruta fresca, con valores de acidez que fluctúan entre 2,02 a 32,89 meq NaOH en 100 g de fruta fresca por lo que el fruto no presenta una acidez definida.
4.2. Humedad de la pulpa de murta azucarada post secado
El porcentaje de sólidos secos de la mezcla de pulpa de murta y azúcar fue determinado antes del proceso de secado y una vez terminado el proceso. Con el porcentaje de sólidos totales post secado se calculó el contenido de masa seca o de sólido seco que presenta cada uno de los tratamientos, lo que permite la determinación del contenido de humedad de los mismos. Las características de la mezcla azucarada posterior al secado que presenta cada tratamiento corresponden a las características de las láminas de fruta respecto a su contenido de humedad. Los valores obtenidos corresponden al promedio de seis repeticiones, los que se presentan en el CUADRO 5. Se aprecia que los cuatro tratamientos presentan un porcentaje inicial similar de sólidos totales, debido a que los tratamientos presentan la misma composición inicial (85 % de murta y 15 % de azúcar) antes del proceso de secado. Sin embargo, el porcentaje de sólidos totales obtenidos después de la deshidratación presenta una leve variación de los valores promedio, lo que puede deberse a las distintas condiciones de proceso (temperatura, espesor del puré) a que son sometidos los distintos tratamientos durante el secado o debido a una variación natural propia del producto (proceso de difusión al interior del sólido), lo que hace que el proceso de evaporación no sea homogéneo entre tratamientos. Los ensayos fueron realizados en estufa de convección natural hasta un porcentaje de humedad final de un promedio de 15,4 ± 1,1% en las láminas de fruta, aunque el valor de humedad según MERINO (2002) puede alcanzar un porcentaje de 7,1 ± 0,5 % para una misma composición inicial de muestra (85 % de murta y 15 % de azúcar), cuando el secado se lleva a cabo en un secador
CUADRO 5. Características de la mezcla azucarada antes y después del proceso de secado.
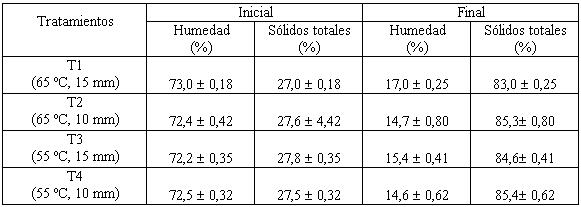
de convección forzada con recirculación de aire. Valores de humedad reportados por SAENZ et al. (2003)Note5. , son del rango de 12 a13 % en láminas deshidratadas. ITDG (2003)Note6. señala contenidos de humedad hasta un 25 % en láminas de fruta, si éstas se acompañan de un alto contenido de azúcar. Por lo cual, el producto obtenido en este estudio puede ser considerado como una lámina deshidratada, ya que están dentro de un rango de humedad citados en la literatura.
4.3.Determinación experimental de la variación de humedad durante el proceso de secado
El experimento consistió en la determinación de la pérdida de peso de la mezcla durante un lapso de tiempo de alrededor de 50 h hasta alcanzar prácticamente el peso constante. Durante las primeras 30 h se determinó la pérdida de peso a un intervalo de tiempo de 1 hora. A partir de la ecuación 3.1 y considerando los valores de masa seca de cada muestra, se calculó el contenido de humedad promedio de las muestras de fruta con respecto a la masa seca (MH / MS) en cada intervalo de tiempo.
4.3.1. Variación de la humedad en función del tiempo En la FIGURA 3, se muestran las curvas de secado de las láminas de fruta para la humedad promedio (MH / MS) en función del tiempo en los diferentes tratamientos (T1, T2, T3, T4). Al observar el comportamiento de secado, las curvas muestran una tendencia de forma polinomial de segundo grado, siendo ésta la que se ajusta con mayor precisión a cada uno de los tratamientos. La humedad varía en función del tiempo desde un valor entre 2,7 y 2,9 kg agua / kg de masa seca hasta un promedio de 0,18 kg agua / kg de masa seca después de las 30 horas de secado. En los tratamientos T1 y T3 con espesor S1 igual a 15 mm, la masa seca varía alrededor de 26 g /100 g de masa húmeda, y en los tratamientos T2 y T4 con un espesor S2 igual a 10 mm la masa seca varía alrededor de lo 18 g / 70 g de masa húmeda.
4.3.2. Comportamiento de secado en los distintos tratamientos. Es posible apreciar una similitud en las curvas correspondiente a cada tratamiento (FIGURA 3), con su coeficiente de correlación cercano a 1. El polinomio correspondiente a cada una de las curvas es válido hasta un tiempo de secado donde la humedad alcanza su valor mínimo, es así como el tratamiento T2 es válido hasta la hora 24de proceso, a partir de este punto la función toma el valor de humedad final. Lo mismo sucede con el tratamiento T4, donde la humedad alcanza su valor casi constante ya en la hora 26, lo que indica que la difusión del agua hacia la superficie del sólido se ve fuertemente reducida a partir de este momento, comenzando las muestras a alcanzar el valor de humedad de equilibrio, así se aprecia en las gráficas correspondientes a los tratamientos señalados.
FIGURA 3. Contenido de humedad en función del tiempo de secado para los cuatro tratamientos.
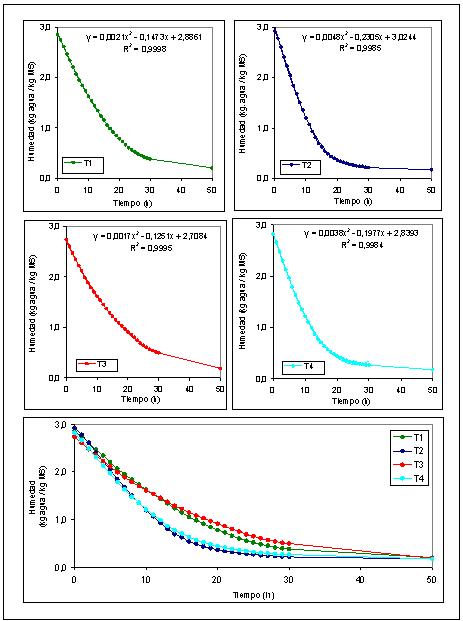
En el caso del tratamiento T1 y T3 la función toma el valor mínimo después de un tiempo de proceso de alrededor de 36 horas, lo que corresponde al valor de la humedad de equilibrio. Esta diferencia en tiempo de secado entre cada tratamiento tiene relación directa con el espesor de la muestra. Tratamientos T1 y T3 con mayor espesor presentan un tiempo superior de secado para alcanzar el valor de humedad de equilibrio, y a su vez los tratamientos T2 y T4 con menor espesor de muestra requieren de menos tiempo para alcanzar dicha humedad. Al observar la gráfica inferior de la FIGURA 3, se logra apreciar claramente el comportamiento de secado que presentan cada uno de los tratamientos. Tratamientos T2 y T4 con menor espesor presentan un comportamiento similar en sus curvas, que lo diferencia claramente de los tratamientos con mayor espesor. Durante las primeras 10 horas de secado ambos tratamientos presentan una variación de humedad similar en el tiempo, la cual indica que el proceso de secado no depende de las temperaturas de trabajo en este intervalo, luego las curvas comienzan a separase y a medida que transcurre el tiempo empiezan a diferenciarse T2 y T4 y el proceso se ve influenciado por las temperaturas de secado. Respecto a los tratamientos T1 y T3, con mayor espesor de muestra y temperaturas de secado igual a 65 y 55 ºC, se aprecia un comportamiento similar de secado debido al espesor de la muestra. Sin embargo a medida que el tiempo avanza comienzan a diferenciarse ambos tratamientos, siendo la temperatura de secado la que marca tal diferencia. También se observa que la variación de humedad correspondiente a T2 y T4 es más acelerada durante las primeras horas de secado, debido al menor espesor que presenta la muestra, por lo cual el contenido local de humedad presente recorre una menor distancia hacia la superficie de evaporación, si se compara con los tratamientos T1 y T3, con mayor espesor para una misma superficie de secado.
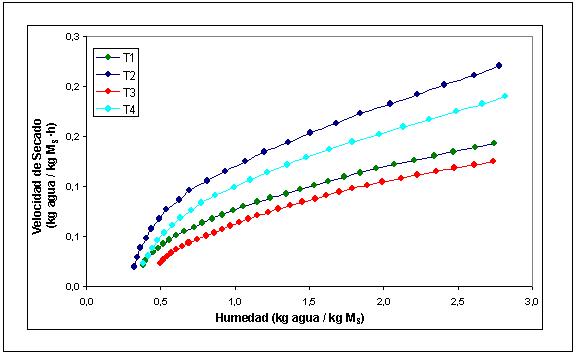
4.3.3. Velocidad de secado en los distintos tratamientos. En la FIGURA 4, se presentan las curvas de velocidad de secado en función de la humedad, donde la ausencia del periodo de velocidad constante se hace evidente al observar las curvas de secado correspondiente a cada uno de los tratamientos, siendo el periodo de velocidad decreciente el que predominó en todo el proceso. La velocidad de secado fue determinada entonces a partir del punto crítico que corresponde a la velocidad máxima de secado, la cual fue calculada según se define en ecuación 3.3. La velocidad de secado aumenta con la temperatura, pero disminuye a medida que el espesor de la muestra aumenta, así se aprecia al observar las curvas correspondiente a los cuatro tratamientos. Por lo cual la velocidad de secado es directamente proporcional a la superficie de secado, e inversamente proporcional al espesor.
FIGURA 4. Curvas de velocidad de secado en función de la humedad promedio para los cuatro tratamientos.
4.4. Determinación de los parámetros de proceso
A partir de las curvas de secado con la humedad promedio en función del tiempo se determinaron los parámetros de proceso, que permiten describir el comportamiento de secado del producto. El tiempo y humedad crítica, la constante de tiempo, humedad de equilibrio y la velocidad máxima de secado correspondiente a cada uno del los tratamientos se presentan en el CUADRO 6.
| Tratamientos |
|
||||||||||||||||
| T1 (65 ºC 15 mm) | 1 | 2,7470 | 18,8 | 0,2048 | 0,1431 | ||||||||||||
| T2 (65 ºC 10 mm) | 1 | 2,7799 | 12,8 | 0,1747 | 0,2209 | ||||||||||||
| T3 (55 ºC 15 mm) | 1 | 2,6120 | 20,9 | 0,1879 | 0,1217 | ||||||||||||
| T4 (55 ºC 10 mm) | 1 | 2,6628 | 14,1 | 0,1755 | 0,1901 | ||||||||||||
Punto crítico. Se observa en el CUADRO 6, un mismo valor de tiempo crítico igual a la primera hora de secado para cada tratamiento, lo que indica que el proceso no consta del primer periodo de secado, o sea, no hay velocidad constante durante el proceso de secado. El tiempo crítico tiene directa relación con la humedad crítica, la cual varía con el espesor del material y con la velocidad de secado (McCABE et al. 1991). Esto muestra diferencias en el punto de inicio del proceso de secado, y como se puede observar en la FIGURA 3 corresponden a 4 diferentes modelos para el proceso de secado. A partir de este momento comienza el periodo de velocidad decreciente.
Constante de tiempo. Se determinó la constante de tiempo según ecuación 3.2, y tal como era de esperarse los tratamientos con mayor espesor presentan una constante de tiempo superior a aquel tratamiento con menor contenido de muestra. También se observa en los valores de la constante de tiempo la influencia de la temperatura sobre cada tratamiento, esto debido a la diferencia de tiempo de proceso que presenta aquellos tratamientos con igual espesor de lámina y distinta temperatura de secado.
Humedad de equilibrio.Con respecto a la humedad de equilibrio esta fue determinada a partir del contenido de sólido seco calculado al final del proceso de secado para cada tratamiento, siendo los tratamientos con mayor espesor los que presentan un mayor contenido de humedad de equilibrio al finalizar el proceso.
Velocidad máxima de secado. Tratamientos con menor espesor de muestra corresponden los valores de mayor velocidad de secado, siendo T2 el que presenta la mayor velocidad de secado con una temperatura de 65 ºC, le sigue el T4 con temperatura de secado de 55 ºC y a continuación tratamientos T1 y T3 con un espesor de muestra mayor y temperaturas de secado de 65 y 55 ºC. Por lo cual la velocidad de secado es directamente proporcional a la superficie de secado, e inversamente proporcional al espesor.
4.5.Simulación del proceso de secado
4.5.1. Determinación del comportamiento del aire de secado. El conocimiento de la condición del aire de secado es de gran importancia en procesos de deshidratación, ya que las propiedades físicas del aire afectan de manera directa sobre la calidad del secado, por lo cual es necesario llevar un control de las variables involucradas, como son: temperatura y humedad relativa del aire de secado. Debido a que fue difícil llevar un control de tales variables se realizó un proceso de simulación para cuantificar el comportamiento del aire durante el tiempo en que duró el experimento. Tal simulación consistió en determinar la variación de la humedad del aire de secado que se produce debido a que el experimento no se realizó con un exceso de aire y además a la abertura de la estufa que se realiza al momento de pesar las muestras.
A continuación en la FIGURA 5, se presenta un diagrama descriptivo del proceso simulado para la determinación del aire de secado.
FIGURA 5. Diagrama descriptivo del proceso simulado.
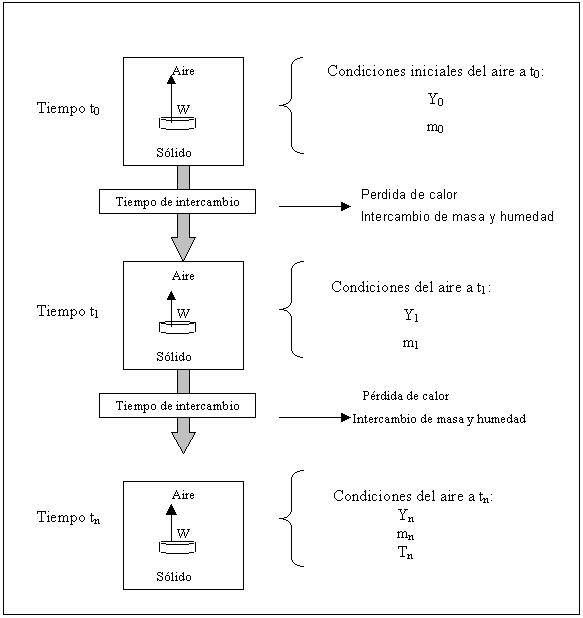
El proceso de simulación involucró las siguientes consideraciones y cálculos:
Consideraciones:
- Condiciones físicas de la estufa de secado: área, volumen
- Condiciones físicas del aire de secado: coeficiente convectivo calor, calor específico, conductividad y difusividad térmica, densidad, y temperatura de bulbo seco
- Condiciones ambientales: temperatura ambiente, humedad relativa
Cálculos:
- Tiempo de intercambio de la masa de aire
- Temperatura del aire de secado al tiempo de intercambio
- Pérdida de calor al tiempo de intercambio
- Pérdida de masa al tiempo de intercambio
Estas permiten la determinación de las masas de aire que salen e ingresan a la estufa en el tiempo de intercambio con sus respectivas humedades, junto con la determinación de la humedad del aire de secado entre cada hora en que se produce la pesada de la muestra, y por tanto la abertura de la puerta. En el ANEXO 1, se presenta una descripción de los pasos a seguir para dichos cálculos. El CUADRO 7, muestra los resultados de la variación que experimenta el aire al tiempo de intercambio, donde se observa que al finalizar la primera hora de secado el aire presenta una humedad relativa de 85 % con una temperatura de secado de 65 ºC, luego al tiempo de intercambio que es igual a 15 s (tiempo de pesada) la temperatura disminuye a 58,7 ºC, debido al intercambio de masa con el medio externo, junto con la pérdida de calor del aire de secado. Ya en la segunda hora la masa y la humedad del aire aumentan, debido al agua evaporada por tiempo de secado y al intercambio de humedad producido durante la pesada, con una humedad relativa de secado de 89 %. Hacia las últimas horas de proceso la humedad relativa del aire disminuye junto con la disminución del agua presente en el sólido, tal como se observa en las curvas de la FIGURA 6.
| Parámetros | Unidades | t0 | t1 | t2 | tn |
| Temperatura aire de secado | ºC | 65 | 65 | 65 | 65 |
| Masa de aire de secado | g | 40 | 45 | 47 | 41 |
| Humedad relativa aire de secado | % | 80 | 85 | 89 | 15 |
| Tiempo de intercambio | s | 15 | 15 | 15 | 15 |
| Pérdida de calor al tiempo de intercambio | J | 140,47 | 140,47 | 140,47 | 140,47 |
| Temperatura al tiempo de intercambio | ºC | 58,7 | 58,7 | 58,7 | 58,7 |
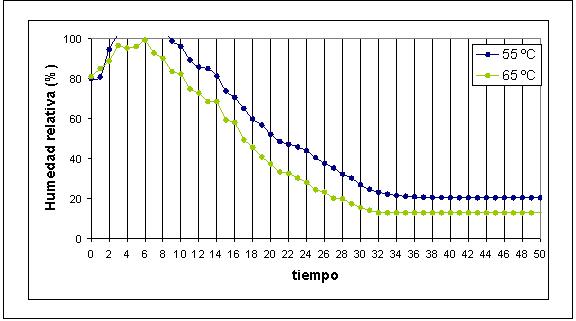
4.5.2. Representación gráfica del comportamiento del aire de secado. La FIGURA 6, representa el comportamiento de la humedad relativa del aire de secado en función del tiempo, donde se aprecia un comportamiento similar para ambas temperaturas de secado durante el transcurso del proceso. Sin embargo, el aire de secado a 55 ºC presenta una humedad de saturación entre la hora 3 y 8 de secado, lo que indica que durante este lapso de tiempo la transferencia de humedad del cuerpo al aire es nula. Luego la humedad relativa del aire comienza a disminuir, junto con la disminución del agua presente en el sólido para ambas condiciones, hasta alcanzar una humedad constante de un 20 % para el secado de 55 ºC y una humedad de 15 % en el secado con aire a 65 ºC. A partir de la hora 31, y hasta el momento en que las muestras son retiradas de la estufa la humedad del aire de secado permanece constante. No hay intercambio de aire debido a que las muestras durante este periodo de tiempo permanecen en las estufas cerradas. La condición del aire se mantiene constante hasta el final del proceso, lo que se puede interpretar también con el término del proceso de secado.
FIGURA 6. Humedad relativa del aire de secado a temperaturas de 55 y 65ºC.
4.6.Parámetros cinéticos adimensionales
El uso de parámetros adimensionales permite relacionar los datos de los diferentes ensayos, reduciendo el número de variables y en consecuencia el número de ensayos necesarios para entender el comportamiento de un proceso. En este trabajo, el cálculo de los parámetros característicosde proceso, tales como punto crítico, constante de tiempo, humedad de equilibrio y velocidad máxima permiten modelar adecuadamente el proceso de secado.
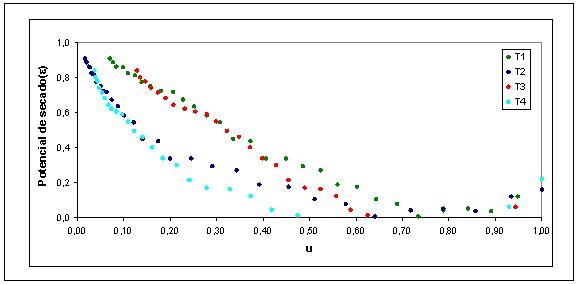
4.6.1. Parámetros adimensionales para humedad y tiempo. Se determinó la humedad (u) y tiempo adimensional () para cada uno de los tratamientos a partir del punto crítico para el periodo de velocidad decreciente. Con las ecuaciones 3.4 que define la humedad adimensional y según ecuación 3.5 correspondiente al tiempo adimensional se obtuvieron los valores adimensionales de los ensayos, los cuales se presentan en la gráfica 1 de la FIGURA 7.
FIGURA 7. Curvas adimensionales de variación de humedad en función del tiempo de secado.
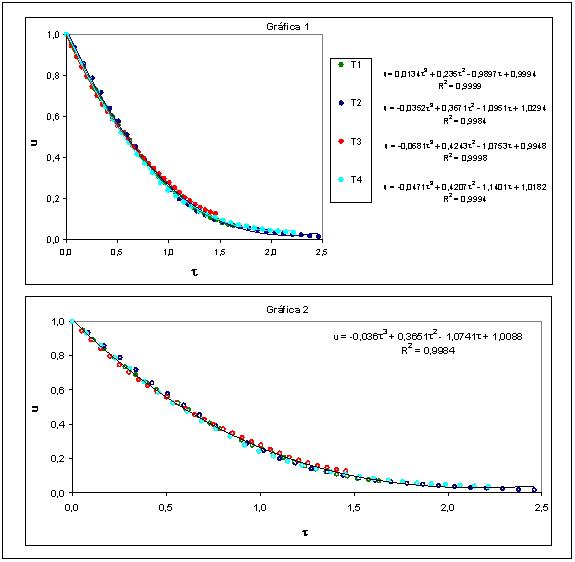
Se ve claramente al observar la gráfica 1, una superposición correspondiente a las curvas de los cuatro tratamientos, por lo cual la variación adimensional de la humedad en función del tiempo no hace diferencia respecto de las condiciones de proceso, ya sea espesor de muestra o temperatura de secado, al contrario de lo que sucede al trabajar con valores de humedad y tiempo absolutos donde existe una clara diferencia entre tratamientos (FIGURA 3). Esta similitud en comportamiento permite relacionar los datos de los distintos tratamientos y obtener una curva común del proceso de secado tal como se presenta en la gráfica 2 de la FIGURA 7. Debido a que se trata de un mismo producto en todos los tratamientos era de esperarse que el comportamiento sea similar bajo cualquier condición de secado. Esto se confirma, ya que los datos obtenidos en los diferentes ensayos se pueden expresar en una curva común (gráfica 2) con un alto coeficiente de correlación muy cercano al valor 1. Se obtiene así una función polinomial, la cual es valida para valores deentre 0 y 2,16. Para un tiempo adimensional mayor, la humedad toma el valor mínimo,. El polinomio obtenido es similar a cada uno de los polinomios de los ensayos por separados (gráfica 1) y corresponde por tanto a un promedio de los resultados de los cuatro experimentos de secado.
4.6.2. Potencial de secado. Considerandoque el experimento cinético clásico se vio afectado por las condiciones exteriores variables es que se introduce un nuevo parámetro adimensional conocido como potencial de secado.
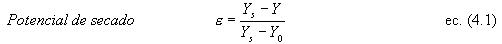
Este parámetro permite conocer el comportamiento de secado que presenta el producto respecto a la humedad del aire de secado. El potencial de secado fue determinado para el transcurso del proceso en ambas estufas, para la condición de secado de 55 y 65 ºC. En la FIGURA 8, se representa el potencial de secado para ambas temperaturas en función del tiempo. Un potencial de secado , significa que el aire de secado tiene una capacidad máxima de secado, mientras el valor de = 0, presenta una mínima. Así se observa en las curvas correspondientes a ambas temperaturas. En el caso de secado con aire a 55 º C entre la hora 3 y 8 de secado el potencial presenta un valor igual a cero, que indica que el secado durante este tiempo es mínimo, debido a que durante estas horas la humedad relativa del aire se encuentra saturada, lo que hace que el proceso de transferencia sea nulo.
FIGURA 8. Potencial de secado en función del tiempo.
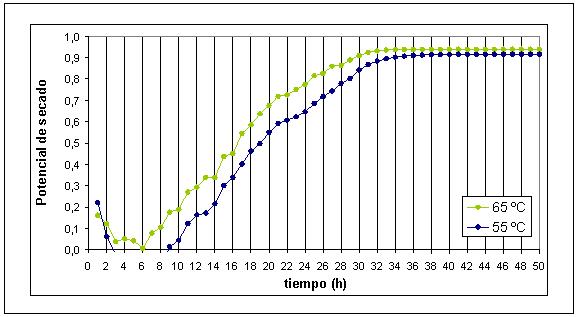
Se realizó además una representación del comportamiento que presenta el potencial de secado respecto a la humedad del producto, por lo cual, se obtuvo un perfil del potencial de secado para cada condición de trabajo, la cual se presenta en las curva de la FIGURA 9. Durantes las primeras horas de secado el producto presenta un mayor contenido de humedad, lo que corresponde además a un mayor porcentaje de agua evaporada por hora de secado, presentando el potencial de secado valores menores al inicio del proceso, debido a un alto porcentaje de humedad presente en el aire de secado (FIGURA 6), a medida que la humedad del sólido comienza a disminuir, disminuye la humedad del aire de secado, con lo cual el potencial de secado aumenta. A primera vista se aprecia un comportamiento similar para cada una de las curvas correspondiente a cada tratamiento, pero a la vez la influencia que tiene el espesor de la muestra sobre comportamiento que presenta el potencial de secado se hace presente diferenciando cada una de las curvas. Es así como tratamientos con mayor espesor de lámina, presentan los mayores valores de potencial hacia el final del proceso, si se compara con las curvas de los tratamientos T2 y T4, con menor espesor para una misma humedad del producto, lo que tiene relación con la velocidad de secado que presenta cada uno de los tratamientos, y por tanto al agua evaporada por tiempo de secado.
FIGURA 9. Potencial de secado en función de la humedad adimensional.
Por lo cual el potencial de secado se relaciona directamente con la humedad del sólido en el momento en que el agua sale de el, y como esta influye en el comportamiento que presenta el aire de secado. Es posible apreciar que tratamientos T3 y T4 a temperatura de secado de 55 ºC, presentan valores de potencial igual a cero, lo que indica una saturación del aire de secado, como se observó en las curvas de la FIGURAS 6 y 8.
4.6.3 Velocidad real de secado y el modelo cinético. A partir del polinomio obtenido en la FIGURA 7, correspondiente a la humedad (u) en función del tiempo (se determinó la velocidad real () para el proceso de secado, la cual se define según ecuación 3.6. La curva correspondiente a la FIGURA 10, representa el comportamiento adimensional de velocidad de secado de la lámina de fruta deshidratada a partir de pulpa de murta azucarada, como una función de la humedad del producto.
FIGURA 10. Velocidad real de secado en función de la humedad adimensional.
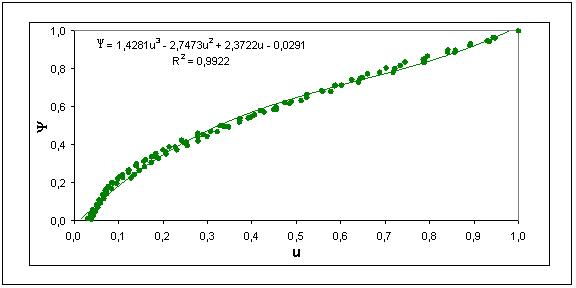
Es así como se obtiene un modelo cinético adimensional (ecuación. 4.2) que representa el comportamiento de secado de un producto, el cual corresponde a una función polinomial de tercer grado, válido para valores de u entre 1 y 0,02 a valores menores de humedad la velocidad alcanza valores negativos, lo que indicaría el efecto higroscópico que presentaría una lámina de fruta hacia las últimas horas de secado. Experimentalmente se ha podido demostrar que al final del proceso de secado, se obtiene un contenido de agua en el producto casi constante lo que corresponde también a una velocidad real de secado igual a cero. Por tanto el modelo tiene su validez sólo hasta la humedad de equilibrio, lo que corresponde en el caso de la lámina de murta a una humedad promedio u igual a 0,02. He aquí la validez de la ecuación 4.2
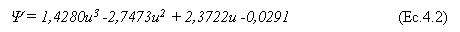
Se tiene entonces un modelo general de secado visualizando como fuerza impulsora la humedad adimensional del aire de secado (ecuación 4.3), la cual se complementa con el potencial de secado
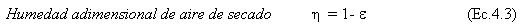
Por tanto la humedad adimensional del aire de secado y a su vez el potencial de secado son función de la humedad adimensional del sólido, tal como se demostró en las curvas de la FIGURA 9. Siendo la velocidad real de secado una función independiente de cualquier condición no constante del proceso, y que sólo depende de la humedad adimensional (u) del producto que se ha secado.
4.7.Determinación del calor específico
El calor específico de una sustancia, es una propiedad termofísica de importancia en procesos térmicos, que en conjunto con la conductividad térmica y la densidad determinan la velocidad de transferencia de calor al interior del producto. Se determinó el calor específico de pulpa de murta azucarada por el método de enfriamiento y por modelos de cálculos existentes en literatura.
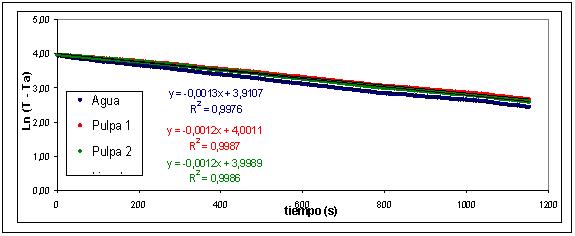
4.7.1. Método de enfriamiento. En la FIGURA 11, se observa una representación gráfica de Ln (T – Ta) en función del tiempo para la pulpa de murta y agua, que se realizó a partir de los datos de enfriamiento obtenidos en la parte experimental. A través de las gráficas se obtuvo el valor de la pendiente (k) correspondiente a cada muestra. Junto con los datos presentados en el CUADRO 8, y según ecuación (3.13) se determinó el calor específico de la pulpa de murta azucarada.
FIGURA 11. Curvas de enfriamiento y valor de la pendiente (k).
| Mediciones | Unidades | Valores |
| kagua | 0,0013 | |
| k1pulpa | 0,0012 | |
| k2pulpa | 0,0012 | |
| Masa agua(MH2O) | kg | 0,0501816 |
| Masa pulpa1 (Mm) | kg | 0,0564163 |
| Masa pulpa2 (Mm) | kg | 0,0564074 |
| Masa cilindro de cobre (Mcu) | kg | 0,2040607 |
| Calor específico agua (CpH2O) | kJ/kg K | 4,1868 |
| Calor específico cobre (Cpcu) | kJ/kg K | 0,383 |
4.7.2. Modelos existentes en literatura
Se estimó el calor específico de la pulpa de murta azucarada mediante relaciones empíricas, modelos basados en la humedad o composición proximal.


A continuación se presenta en el CUADRO 9, lo valores de calor específico obtenidos por los modelos anteriormente mencionados.
| Método | calor específico (kJ/ kg K) |
Factor |
| Ley de enfriamiento de NEWTON Muestra 1 Muestra 2 |
2,32 2,32 |
1 1 |
| CHOI Y OKOS a 55 ºC a 65 ºC |
3,52 3,51 |
1,5 1,5 |
| DICKERSON | 3,49 | 1,5 |
| SIEBEL | 3,26 | 1,4 |
| CHARM | 3,46 | 1,5 |
Como es posible apreciar en el cuadro anterior existe una diferencia en el valor del calor específico obtenido experimentalmente, y aquellos obtenidos por modelos existentes en literatura, con un factor de diferencia mayor de 1,5 en caso de CHOI Y OKOS y un factor menor de 1,4 en caso de SIEBEL. Esta diferencia puede estar dada debido a las condiciones experimentales. La incorporación de aire que se produce al momento de mezclar el contenido de azúcar en la pulpa de murta para la obtención de una muestra homogénea, puede haber influido en forma significativa en el volumen de mezcla a utilizar al momento del ensayo, influyendo además en el valor de calor específico obtenido.Respecto a la diferencia de calor específico entre modelos encontrado en literatura, esta se debe a que algunos autores en sus modelos empíricos solo consideran la humedad del producto y otros como CHOI Y OKOS, consideran dentro del modelo la composición proximal para una misma estimación de calor específico. Sin embargo, ambos modelos suministran resultados satisfactorios bajo cierta condición de temperatura y humedad. LAGOS (2002) determinó el calor específico en pasta de murta, mediante el método de las mezclas obteniendo un valor de 3,47 kJ / kg K, y al estimar el calor especifico de la pasta de murta según CHOI Y OKOS, se obtiene un valor de 3,73 kJ / kg K, el cual es mayor que el valor obtenido en pulpa de murta azucarada utilizando igual método de estimación. Este menor valor de calor específico en pulpa de murta tiene relación con el menor contenido de humedad que presenta la pulpa azucarada respecto a la pasta de murta, ya que a medida que el contenido de agua decrece, el calor específico también disminuye. La presencia de aire en la pulpa azucarada, la cual es un material poroso es la causa más probable que el calor específico determinado experimentalmente no coincida con lo valores estimados en literatura, en los cuales no se considera el efecto del contenido del aire en las muestras. En cálculos de consumo energético más detallados se podría considerar el efecto del aire sobre el calor específico de las muestras, pero en cálculos iniciales estimativos para un proyecto de factibilidad económica , es suficiente utilizar modelos de cálculos existentes en literatura . No obstante, el método de enfriamiento de Newton puede entregar valores de calor específicos que se aproximan mejor a la de condiciones reales de procesamiento de un producto como láminas de murta. Será necesario implementar más ensayos para obtener datos válidos estadísticamente.
4.8. Estimación del consumo energético
Para la estimación del consumo energético en la deshidratación de una lámina de fruta, se consideró cada uno de los tratamientos y se evaluó su comportamiento energético bajo distintas condiciones de secado, como la humedad del aire, temperatura de secado y espesor del puré. Se consideraron humedades relativas del aire de secado de 80, 60 y 40% y temperaturas de secado de 65 y 55 ºC (condiciones constantes de proceso). A partir de la ecuación 4.4 que define el coeficiente de vaporización (kg aire/ m2h) y según ecuación 4.5 correspondiente al flujo de calor (kJ / m2h), se estimó el consumo energético en la deshidratación de una lámina de fruta bajo condiciones constantes de proceso (FIGURA 12).
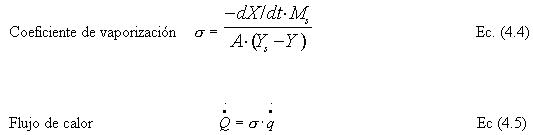
FIGURA 12. Consumo energético de los cuatro tratamientos bajo distintas condiciones del aire de proceso.
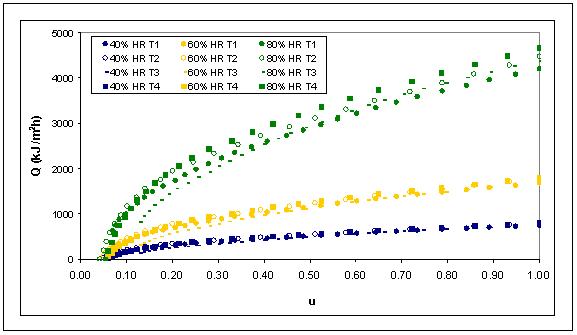
El comportamiento energético estimado se refleja claramente en la curvas de la FIGURA 12, donde se observa que el secado con aire a 80% de humedad relativa, es el que más consume energía, lo cual está dentro de la lógica esperada, debido a que a mayor humedad del aire de secado mayor será el tiempo requerido para la deshidratación de un producto, y por tanto mayor el gasto de energía. Luego con un gasto energético menor se encuentra el secado con aire a 60 y 40 % de humedad relativa. Se observa además en cada una de las curvas que la condición de temperatura y espesor que presentan cada uno de los tratamientos no es significativo en el gasto energético, como si lo es la condición de humedad del aire de secado. Como es de esperarse, a medida que la humedad del producto disminuye el gasto energético también disminuye.
Tiempo de secado: En la determinación del tiempo de secado de la lámina de fruta deshidratada, se utilizó el método de integración gráfica en la que el valor inverso de la velocidad () se representa en función del contenido de humedad (u). (GEANKOPLIS 1986).
FIGURA 13. Representación gráfica del inverso de la velocidad en función de la humedad.
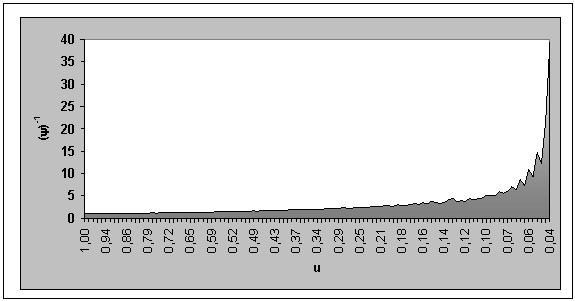
Por lo que el tiempo de secado para cualquier región entre u1 y u2 está dado por la ecuación 4.6
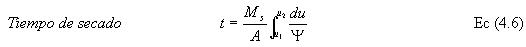
Por tanto, el tiempo promedio estimado para la deshidratación de la pulpa de murta azucarada con una humedad inicial de 73 % y una humedad promedio final en la lámina deshidratada de 15 % es de 11,5 horas de secado bajo condición constante de proceso.
Cálculos energéticos: Con un balance simple de materia y energía y mediante el uso del diagrama de Mollier, se determinó la temperatura de la superficie del producto, la temperatura del aire de calentamiento, y el consumo de vapor para distintas condiciones de proceso.
Condiciones de proceso:
Estado del aire fresco: 20 ºC, 90% HR
Estado del aire a la salida: 40 ºC, 40, 60 y 80% HR
Cantidad de pulpa a secar: 1000 kg / h
Humedad inicial de la pulpa de fruta: 73%
Humedad final de la lámina de fruta deshidratada: 15%
Balance de materia: Se determinó la cantidad de agua evaporada por hora de secado, donde W = 682 kg agua evaporada/h y por tanto la cantidad de producto deshidratado es igual a 318 kg de láminas por hora de secado.
| PARAMETROS | UNIDADES |
|
||||||||
| Entalpía | KJ/ kg aire seco | 87 | 113 | 138 | ||||||
| Temperatura superficie | º C | 28 | 32 | 37 | ||||||
| Temperatura aire calentamiento | º C | 53 | 76 | 102 | ||||||
| Consumo de vapor | KJ / h | 59334 | 77066 | 94116 | ||||||
Los valores energéticos estimados indican que la condición del aire de secado es uno de los parámetros fundamentales a considerar al momento de deshidratar un producto, tal como se aprecia en el CUADRO 10, valores de entalpía estimados señala un gasto mayor en kJ por kg de aire seco para la condición de humedad relativa 80 % y a la vez un mayor consumo de vapor por hora de secado, junto con un aumento de la temperatura de calentamiento. A medida que la humedad del aire disminuye, la entalpía, la temperatura de calentamiento y consumo de vapor requerido para el proceso de secado se ve fuertemente reducido.
5. CONCLUSIONES
- Es posible obtener un modelo de secado para la deshidratación de láminas de fruta a través de un método cinético experimental
- La determinación de la cinética de secado utilizando parámetros adimensionales resultó ser un método efectivo que permite modelar adecuadamente el proceso de secado bajo distintas condiciones de proceso.
- El modelo cinético tiene como variable sólo la velocidad real de secado como función de la humedad adimensional del producto, siendo la humedad del aire de secado la fuerza impulsora que rige el proceso de secado; la temperatura de secado y espesor del producto no influyen sobre el modelo, ya que están incluidos en los parámetros adimensionales
- El modelo es aplicable para cualquier temperatura o espesor de lámina.
- El valor de calor específico de la pulpa de murta azucarada obtenido por el método de enfriamiento de Newton difiere a los valores estimados por modelos existentes en literatura, por lo que el método de enfriamiento de Newton entregó resultados que consideran la inclusión del aire en pulpa de murta azucarada.
- El gasto energético en la deshidratación de una lámina de fruta está dado por la condición del aire de secado, siendo la temperatura y espesor variables que no interfieren el consumo energético dentro del rango evaluado.
BIBLIOGRAFIA
- ASSOCIATION OF OFFICIAL ANALYTICAL CHEMISTRY (AOAC). 1995. Official Methods of Analysis of AOAC International. Vol. II. 16th Edition. Cap. 37.
- BELITZ, H. y GROSCH, W. 1997. Química de los alimentos. 2a Edición. Editorial Acribia Zaragoza. España.1087 p.
- CASP, A y ABRIL, J. 1999. Procesos de conservación de alimentos. Ediciones Mundi-Prensa. España. 494p.
- CHARM, S.E. 1971. Fundamental of food engineering. Van Nostrand Reinhold / AVI, New York. 164 p.
- CHOI, Y., y OKOS, M.R. 1986. The thermal properties of tomato juice concentrates. Transactions of the ASAE. 26: 305-311.
- DICKERSON, R. W. JR. 1969. Thermal properties of food. 4th ed., Van Nostrand Reinhold / AVI, New York.
- GEANKOPLIS, C. 1986. Procesos de transporte y operaciones unitarias. Editorial Continental, S.A., México. 759 p.
- HWANG, M., HAYAKAWA, K. 1979. A specific heat calorimeter for foods. J. Food Sci. 44: 435-438.
- KNEULE, F. 1966. El secado. Ediciones Urmo, S.A. Bilbao. España.414 p.
- LAGOS, J. 2002. Determinación del calor específico en pasta de murta (Ugni molinae Turcz), en función de la temperatura. Tesis Ingeniero en Alimentos. Valdivia, Chile. Universidad Austral, Facultad de Ciencias Agrarias. 63 p.
- LAVIN, A y MUÑOZ, C. 1988. Propagación de la murtilla (Ugni molinae Turcz) mediante estacas apicales semi leñosas. Agricultura Técnica 48 (1): 58-59.
- LIDE, R. D. 1999. Handbook of chemistry and physics. CRC Press LLC 80th edition. 3-6 p.
- McCABE, W., SMITH, J. y HARRIOT, P. 1991. Operaciones básicas de Ingeniería Química. Cuarta edición. McGraw-Hill, Inc.1112 p.
- McNAUGHTON, I. L., MORTIMER, C. T. 1975. Calorimetría diferencial de barrido. Physical chemistry. Series 2,10. Perkín Elmer Corporation.
- MERINO, F. 2002. Elaboración de Láminas de Fruta (“Fruit leathers”) a partir de pulpa de murta (Ugni molinae Turcz) congelada. Tesis Ingeniero en Alimentos. Valdivia, Chile. Universidad Austral, Facultad de Ciencias Agrarias. 66 p.
- MOHSENIN, N. M. 1980. Thermal properties of food and agriculture materials. Gordan and Breach. Science publishers. New York. 407p.
- MOYLS, A. 1981.Drying of apple purees. J. Food Sci. 46 (3): 939- 942
- MUÑOZ , J. 2002. Determinación de la difusividad térmica en pasta de murta (Ugni molinae Turcz) en función de la temperatura. Tesis Ingeniero en Alimentos. Valdivia, Chile. Universidad Austral, Facultad de Ciencias Agrarias. 115 p.
- PERRY, J.H. 1958. Chemical Engineers Handbook. 3a Ed., Nueva York
- RODRIGUEZ, G. 1986. Murta (Ugni molinae Turcz). Chile Forestal 11 (127): 33
- SCHMIDT - HEBBEL, H. y PENNACCHIOTTI, I. 1979. Tabla de composición química de los alimentos chilenos. Sexta edición. Editorial Antartica S.A. 20 p.
- SEPULVEDA, C. 1994. Evaluación del comportamiento físico-químico de murtilla (Ugni molinae Turcz) sometido a diferentes temperaturas de congelación y tiempo de almacenaje. Tesis Ingeniero Agrónomo Chillán, Chile. Universidad de Concepción, Facultad de Agronomía. 104 p.
- TORRES, E.; SEGUEL, I.; CONTRERAS, G.; y CASTRO, M.; 1999. Caracterización Físico-Química de Frutas de Murta (Murtilla) Ugni molinae Turcz. Agricultura Técnica 59 (4): 260-270
- VAN ARSDEL, W., COPLEY, M. y MORGAN, A. 1973. Food Dehydration. 2nd Edition. The Avi Publishing Company, Inc.374 p.
- WEISS, S.; MILITZER, K. E.; 1984. Thermische Verfahrenstechnik, Lehrbuch, 3a Edición . VEB Deutscher Verlag für Grundstoff Industrie, Leipzig.
ANEXO
Pasos a seguir para la determinación de la humedad relativa del aire de secado a temperatura de 65 °C
Paso 1: Condiciones físicas de la estufa de secado
Paso 2: Condiciones físicas del aire de secado
- Coeficiente convectivo (h): 11,3 W / m2 K
- Cp entre 0 – 100 ºC (Cp): 1005 J / kg K
- Conductividad térmica (k): 0,02901 W /m K
- Densidad (): 1,063 kg / m3
- Difusividad térmica (α): 2,72·10-5 m2/s
- Temperatura bulbo seco (Ti): 65 ºC
Paso 3: Condiciones ambientales
Paso 4: Cálculos
- Tiempo de intercambio (ti), se determinó el tiempo de intercambio del aire mediante el uso de un cronómetro al momento de abrir la puerta para realizar la pesada, lo que fue igual 15 s
Número de Fourier (Fo), se determinó Fourier al tiempo de intercambio según:

donde χ es igual a 0,1m
Por tanto el valor de Fo al tiempo de intercambio es 0,15
- Temperatura después del intercambio, la siguiente expresión corresponde a una serie infinita de Fourier, la cual permite determinar la temperatura después del intercambio de aire
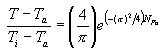
Por tanto el valor de temperatura después del intercambio corresponde a una temperatura de 58,7 ºC
Paso 5: Determinaciones energéticas
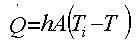
Por tanto el flujo de calor corresponde a 9,36 W
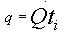
La pérdida de calor para el tiempo de intercambio corresponde a un valor de 140,47J
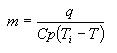
Por tanto la pérdida de masa para el tiempo de intercambio es de 21 g
- Paso 6: condiciones del aire de secado antes de abrir la estufa
- Masa inicial de aire (ma): 40 g
- Agua evaporada (Av): 5,1 g
- Masa de aire (mt) en la estufa después del tiempo t: 45,1 g
- Humedad inicial por kg de aire (Yi): 0,200 kg agua / kg aire seco
- Humedad de saturación (Ys): 0,210 kg agua / kg aire seco
- Humedad de aire en la estufa (Y), según:
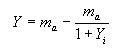
Por tanto la humedad del aire en la estufa corresponde a un valor de 6,69 g
- Humedad total (YT) del aire antes de abrir la estufa, corresponde a la humedad del aire de la estufa más la cantidad de agua evaporada, tal como se expresa:
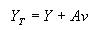
Por tanto, la humedad total corresponde a 11,83 g
Paso 7: condiciones del aire de secado después de abrir la estufa
- Masa de aire no cambiada (mnc), corresponde a la cantidad de aire que permanece en la estufa de secado en el tiempo de intercambio, es decir durante el tiempo en que permanece la puerta abierta. Lo que es igual a:

Entonces la masa de aire no cambiada corresponde a 19 g
- Humedad de aire no cambiada (Ync), corresponde a la cantidad de humedad que permanece en la estufa de secado durante el tiempo de intercambio, según ecuación 4.10 se define como:
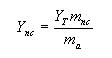
Por lo cual la humedad de aire no cambiada es de 5,66 g
- Humedad en aire cambiada, corresponde a la humedad de aire de intercambio producido durante el lapso en que se mantiene abierta la estufa de secado
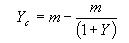
Entonces la humedad de aire cambiada en le tiempo de intercambio corresponde a un valor de 0,31 g
Paso 8: condiciones del aire de secado después de cerrar la estufa
- Humedad del aire en la estufa (Ye): corresponde a la humedad de aire no cambiada más la humedad de aire cambiada.
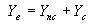
Por lo cual el valor de humedad es de 5.97g
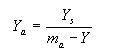
Por lo que el valor de humedad absoluta de aire correspondiente a la primera hora de secado luego de cerrar la puerta es de 0,178 kg agua / kg aire seco y la humedad relativa corresponde a un valor de 85 %.
La determinación de la humedad del aire para las siguientes horas de secado se llevó acabo siguiendo el mismo procedimiento descrito anteriormente reiniciando los cálculo con la condición de secado de la hora anterior.
Note1. 1 Vega, A.; Andrés, A.; Fito, P., 2002a: Influencia de la temperatura en la cinética de secado por aire caliente de pimiento (capsicum annuum L.). Available at: http://cesia2002.udl.es/tc/OB-06.pdf , Accessed: marzo 2003
Note2. Gahona, E., 2002: Deshidratación de frutas y vegetales Available at: http://members.es.tripod.de/egahona/agrono/deshidra.htm. Accessed: marzo 2003
Note3. Intermediate Technology Development Group., ITDG:Available at: www.itdg.org/technical_erquirie/docs/fruit_leathers.pdf. Accessed: octubre 2003
Note4. Determinación de las isotermas de sorción de materiales constructivos porosos e higroscópicos (madera)Available at: www.unne.edu.ar/cyt/2001/7-tegnologicasT-0.38.pdf. Accessed: enero 2004
Note5. 8 SAENZ, A; ESTEVEZ, M; STIER, A., 2003: Dried Fruit Leathers from And Kiwifruit and Apple Pulps
Note6. 9Intermediate Technology Development Group., ITDG:Available at: www.itdg.org/technical_erquirie/docs/fruit_leathers.pdf. Accessed: octubre 2003